Guy Sagi
GSP-KalmanNet: Tracking Graph Signals via Neural-Aided Kalman Filtering
Nov 28, 2023Abstract:Dynamic systems of graph signals are encountered in various applications, including social networks, power grids, and transportation. While such systems can often be described as state space (SS) models, tracking graph signals via conventional tools based on the Kalman filter (KF) and its variants is typically challenging. This is due to the nonlinearity, high dimensionality, irregularity of the domain, and complex modeling associated with real-world dynamic systems of graph signals. In this work, we study the tracking of graph signals using a hybrid model-based/data-driven approach. We develop the GSP-KalmanNet, which tracks the hidden graphical states from the graphical measurements by jointly leveraging graph signal processing (GSP) tools and deep learning (DL) techniques. The derivations of the GSP-KalmanNet are based on extending the KF to exploit the inherent graph structure via graph frequency domain filtering, which considerably simplifies the computational complexity entailed in processing high-dimensional signals and increases the robustness to small topology changes. Then, we use data to learn the Kalman gain following the recently proposed KalmanNet framework, which copes with partial and approximated modeling, without forcing a specific model over the noise statistics. Our empirical results demonstrate that the proposed GSP-KalmanNet achieves enhanced accuracy and run time performance as well as improved robustness to model misspecifications compared with both model-based and data-driven benchmarks.
GSP-Based MAP Estimation of Graph Signals
Sep 23, 2022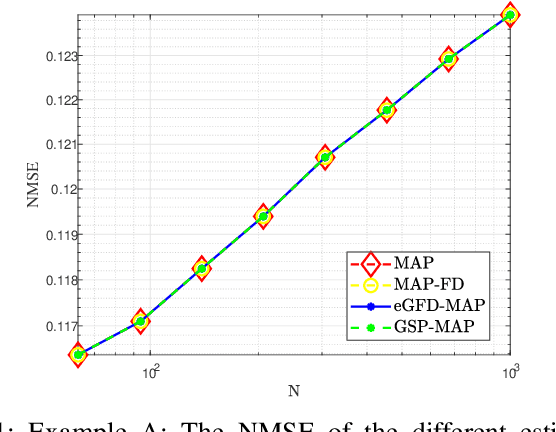
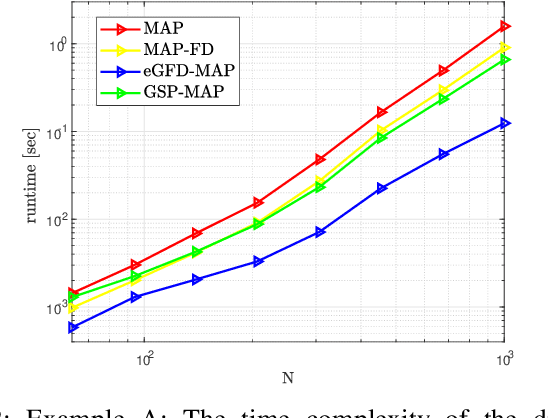
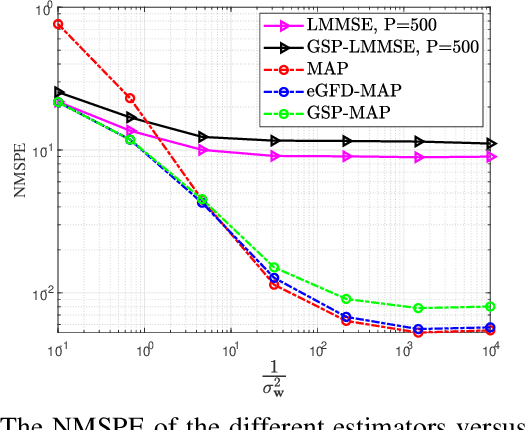
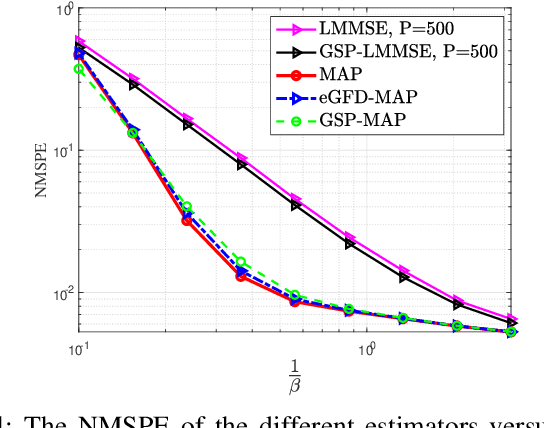
Abstract:In this paper, we consider the problem of recovering random graph signals from nonlinear measurements. We formulate the maximum a-posteriori probability (MAP) estimator, which results in a nonconvex optimization problem. Conventional iterative methods for minimizing nonconvex problems are sensitive to the initialization, have high computational complexity, and do not utilize the underlying graph structure behind the data. In this paper we propose two new estimators that are both based on the Gauss-Newton method: 1) the elementwise graph-frequency-domain MAP (eGFD-MAP) estimator; and 2) the graph signal processing MAP (GSP-MAP) estimator. At each iteration, these estimators are updated by the outputs of two graph filters, with the previous state estimator and the residual as the input graph signals. The eGFD-MAP estimator is an ad-hoc method that minimizes the MAP objective function in the graph frequency domain and neglects mixed-derivatives of different graph frequencies in the Jacobian matrix as well as off-diagonal elements in the covariance matrices. Consequently, it updates the elements of the graph signal independently, which reduces the computational complexity compared to the conventional MAP estimator. The GSP-MAP estimator is based on optimizing the graph filters at each iteration of the Gauss-Newton algorithm. We state conditions under which the eGFD-MAP and GSP- MAP estimators coincide with the MAP estimator, in the case of an observation model with orthogonal graph frequencies. We evaluate the performance of the estimators for nonlinear graph signal recovery tasks with synthetic data and with the real-world problem of state estimation in power systems. These simulations show the advantages of the proposed estimators in terms of computational complexity, mean-squared-error, and robustness to the initialization of the iterative algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge