Can We Break the Curse of Multiagency in Robust Multi-Agent Reinforcement Learning?

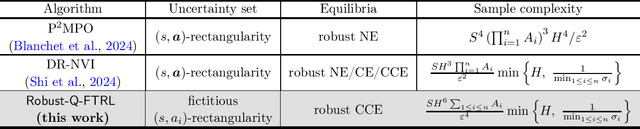
Standard multi-agent reinforcement learning (MARL) algorithms are vulnerable to sim-to-real gaps. To address this, distributionally robust Markov games (RMGs) have been proposed to enhance robustness in MARL by optimizing the worst-case performance when game dynamics shift within a prescribed uncertainty set. Solving RMGs remains under-explored, from problem formulation to the development of sample-efficient algorithms. A notorious yet open challenge is if RMGs can escape the curse of multiagency, where the sample complexity scales exponentially with the number of agents. In this work, we propose a natural class of RMGs where the uncertainty set of each agent is shaped by both the environment and other agents' strategies in a best-response manner. We first establish the well-posedness of these RMGs by proving the existence of game-theoretic solutions such as robust Nash equilibria and coarse correlated equilibria (CCE). Assuming access to a generative model, we then introduce a sample-efficient algorithm for learning the CCE whose sample complexity scales polynomially with all relevant parameters. To the best of our knowledge, this is the first algorithm to break the curse of multiagency for RMGs.

Beyond Weisfeiler-Lehman: A Quantitative Framework for GNN Expressiveness

Designing expressive Graph Neural Networks (GNNs) is a fundamental topic in the graph learning community. So far, GNN expressiveness has been primarily assessed via the Weisfeiler-Lehman (WL) hierarchy. However, such an expressivity measure has notable limitations: it is inherently coarse, qualitative, and may not well reflect practical requirements (e.g., the ability to encode substructures). In this paper, we introduce a unified framework for quantitatively studying the expressiveness of GNN architectures, addressing all the above limitations. Specifically, we identify a fundamental expressivity measure termed homomorphism expressivity, which quantifies the ability of GNN models to count graphs under homomorphism. Homomorphism expressivity offers a complete and practical assessment tool: the completeness enables direct expressivity comparisons between GNN models, while the practicality allows for understanding concrete GNN abilities such as subgraph counting. By examining four classes of prominent GNNs as case studies, we derive simple, unified, and elegant descriptions of their homomorphism expressivity for both invariant and equivariant settings. Our results provide novel insights into a series of previous work, unify the landscape of different subareas in the community, and settle several open questions. Empirically, extensive experiments on both synthetic and real-world tasks verify our theory, showing that the practical performance of GNN models aligns well with the proposed metric.