Fundamental Limits and Tradeoffs in Invariant Representation Learning

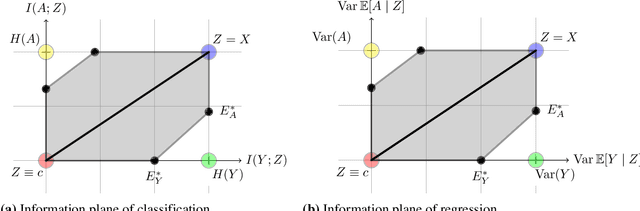
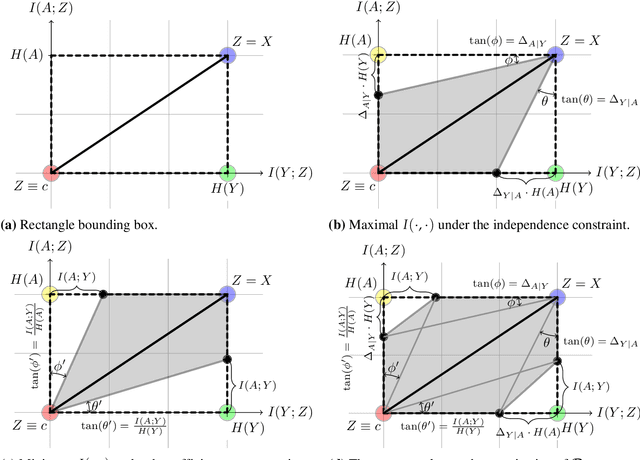
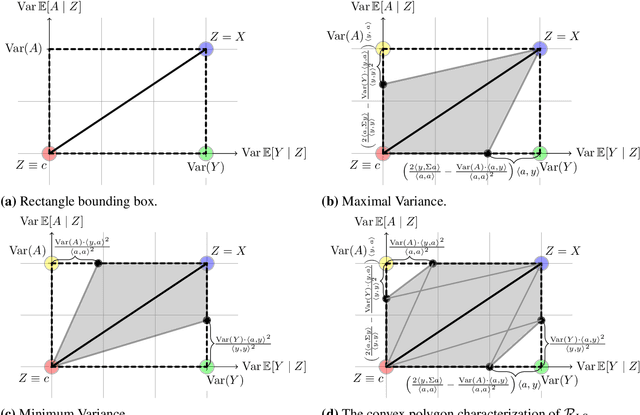
Many machine learning applications involve learning representations that achieve two competing goals: To maximize information or accuracy with respect to a subset of features (e.g.\ for prediction) while simultaneously maximizing invariance or independence with respect to another, potentially overlapping, subset of features (e.g.\ for fairness, privacy, etc). Typical examples include privacy-preserving learning, domain adaptation, and algorithmic fairness, just to name a few. In fact, all of the above problems admit a common minimax game-theoretic formulation, whose equilibrium represents a fundamental tradeoff between accuracy and invariance. Despite its abundant applications in the aforementioned domains, theoretical understanding on the limits and tradeoffs of invariant representations is severely lacking. In this paper, we provide an information-theoretic analysis of this general and important problem under both classification and regression settings. In both cases, we analyze the inherent tradeoffs between accuracy and invariance by providing a geometric characterization of the feasible region in the information plane, where we connect the geometric properties of this feasible region to the fundamental limitations of the tradeoff problem. In the regression setting, we also derive a tight lower bound on the Lagrangian objective that quantifies the tradeoff between accuracy and invariance. This lower bound leads to a better understanding of the tradeoff via the spectral properties of the joint distribution. In both cases, our results shed new light on this fundamental problem by providing insights on the interplay between accuracy and invariance. These results deepen our understanding of this fundamental problem and may be useful in guiding the design of adversarial representation learning algorithms.