Phuc Luong
Improving Random Forests by Smoothing
May 11, 2025Abstract:Gaussian process regression is a popular model in the small data regime due to its sound uncertainty quantification and the exploitation of the smoothness of the regression function that is encountered in a wide range of practical problems. However, Gaussian processes perform sub-optimally when the degree of smoothness is non-homogeneous across the input domain. Random forest regression partially addresses this issue by providing local basis functions of variable support set sizes that are chosen in a data-driven way. However, they do so at the expense of forgoing any degree of smoothness, which often results in poor performance in the small data regime. Here, we aim to combine the advantages of both models by applying a kernel-based smoothing mechanism to a learned random forest or any other piecewise constant prediction function. As we demonstrate empirically, the resulting model consistently improves the predictive performance of the underlying random forests and, in almost all test cases, also improves the log loss of the usual uncertainty quantification based on inter-tree variance. The latter advantage can be attributed to the ability of the smoothing model to take into account the uncertainty over the exact tree-splitting locations.
Improving Robustness and Accuracy of Ponzi Scheme Detection on Ethereum Using Time-Dependent Features
Aug 31, 2023Abstract:The rapid development of blockchain has led to more and more funding pouring into the cryptocurrency market, which also attracted cybercriminals' interest in recent years. The Ponzi scheme, an old-fashioned fraud, is now popular on the blockchain, causing considerable financial losses to many crypto-investors. A few Ponzi detection methods have been proposed in the literature, most of which detect a Ponzi scheme based on its smart contract source code or opcode. The contract-code-based approach, while achieving very high accuracy, is not robust: first, the source codes of a majority of contracts on Ethereum are not available, and second, a Ponzi developer can fool a contract-code-based detection model by obfuscating the opcode or inventing a new profit distribution logic that cannot be detected (since these models were trained on existing Ponzi logics only). A transaction-based approach could improve the robustness of detection because transactions, unlike smart contracts, are harder to be manipulated. However, the current transaction-based detection models achieve fairly low accuracy. We address this gap in the literature by developing new detection models that rely only on the transactions, hence guaranteeing the robustness, and moreover, achieve considerably higher Accuracy, Precision, Recall, and F1-score than existing transaction-based models. This is made possible thanks to the introduction of novel time-dependent features that capture Ponzi behaviours characteristics derived from our comprehensive data analyses on Ponzi and non-Ponzi data from the XBlock-ETH repository
Bayesian Optimization with Missing Inputs
Jun 19, 2020
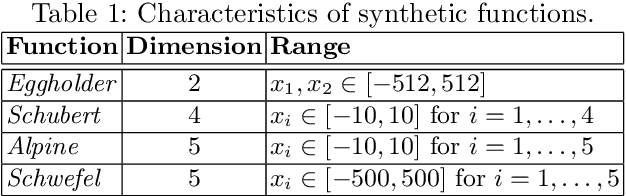


Abstract:Bayesian optimization (BO) is an efficient method for optimizing expensive black-box functions. In real-world applications, BO often faces a major problem of missing values in inputs. The missing inputs can happen in two cases. First, the historical data for training BO often contain missing values. Second, when performing the function evaluation (e.g. computing alloy strength in a heat treatment process), errors may occur (e.g. a thermostat stops working) leading to an erroneous situation where the function is computed at a random unknown value instead of the suggested value. To deal with this problem, a common approach just simply skips data points where missing values happen. Clearly, this naive method cannot utilize data efficiently and often leads to poor performance. In this paper, we propose a novel BO method to handle missing inputs. We first find a probability distribution of each missing value so that we can impute the missing value by drawing a sample from its distribution. We then develop a new acquisition function based on the well-known Upper Confidence Bound (UCB) acquisition function, which considers the uncertainty of imputed values when suggesting the next point for function evaluation. We conduct comprehensive experiments on both synthetic and real-world applications to show the usefulness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge