Improving Robustness and Accuracy of Ponzi Scheme Detection on Ethereum Using Time-Dependent Features

The rapid development of blockchain has led to more and more funding pouring into the cryptocurrency market, which also attracted cybercriminals' interest in recent years. The Ponzi scheme, an old-fashioned fraud, is now popular on the blockchain, causing considerable financial losses to many crypto-investors. A few Ponzi detection methods have been proposed in the literature, most of which detect a Ponzi scheme based on its smart contract source code or opcode. The contract-code-based approach, while achieving very high accuracy, is not robust: first, the source codes of a majority of contracts on Ethereum are not available, and second, a Ponzi developer can fool a contract-code-based detection model by obfuscating the opcode or inventing a new profit distribution logic that cannot be detected (since these models were trained on existing Ponzi logics only). A transaction-based approach could improve the robustness of detection because transactions, unlike smart contracts, are harder to be manipulated. However, the current transaction-based detection models achieve fairly low accuracy. We address this gap in the literature by developing new detection models that rely only on the transactions, hence guaranteeing the robustness, and moreover, achieve considerably higher Accuracy, Precision, Recall, and F1-score than existing transaction-based models. This is made possible thanks to the introduction of novel time-dependent features that capture Ponzi behaviours characteristics derived from our comprehensive data analyses on Ponzi and non-Ponzi data from the XBlock-ETH repository

Committed Private Information Retrieval

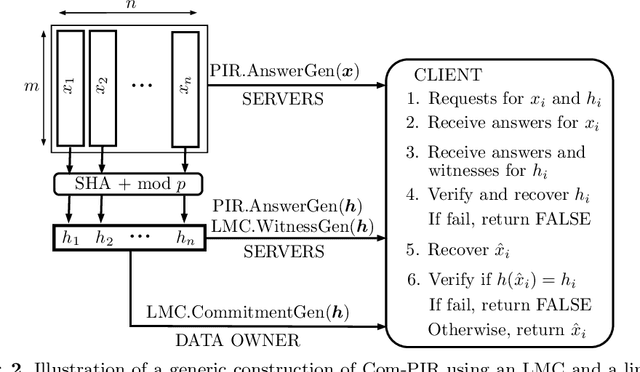
A private information retrieval (PIR) scheme allows a client to retrieve a data item $x_i$ among $n$ items $x_1,x_2,...,x_n$ from $k$ servers, without revealing what $i$ is even when $t < k$ servers collude and try to learn $i$. Such a PIR scheme is said to be $t$-private. A PIR scheme is $v$-verifiable if the client can verify the correctness of the retrieved $x_i$ even when $v \leq k$ servers collude and try to fool the client by sending manipulated data. Most of the previous works in the literature on PIR assumed that $v < k$, leaving the case of all-colluding servers open. We propose a generic construction that combines a linear map commitment (LMC) and an arbitrary linear PIR scheme to produce a $k$-verifiable PIR scheme, termed a committed PIR scheme. Such a scheme guarantees that even in the worst scenario, when all servers are under the control of an attacker, although the privacy is unavoidably lost, the client won't be fooled into accepting an incorrect $x_i$. We demonstrate the practicality of our proposal by implementing the committed PIR schemes based on the Lai-Malavolta LMC and three well-known PIR schemes using the GMP library and \texttt{blst}, the current fastest C library for elliptic curve pairings.