JAPAN: Joint Adaptive Prediction Areas with Normalising-Flows

Conformal prediction provides a model-agnostic framework for uncertainty quantification with finite-sample validity guarantees, making it an attractive tool for constructing reliable prediction sets. However, existing approaches commonly rely on residual-based conformity scores, which impose geometric constraints and struggle when the underlying distribution is multimodal. In particular, they tend to produce overly conservative prediction areas centred around the mean, often failing to capture the true shape of complex predictive distributions. In this work, we introduce JAPAN (Joint Adaptive Prediction Areas with Normalising-Flows), a conformal prediction framework that uses density-based conformity scores. By leveraging flow-based models, JAPAN estimates the (predictive) density and constructs prediction areas by thresholding on the estimated density scores, enabling compact, potentially disjoint, and context-adaptive regions that retain finite-sample coverage guarantees. We theoretically motivate the efficiency of JAPAN and empirically validate it across multivariate regression and forecasting tasks, demonstrating good calibration and tighter prediction areas compared to existing baselines. We also provide several \emph{extensions} adding flexibility to our proposed framework.

Conformalised Conditional Normalising Flows for Joint Prediction Regions in time series

Conformal Prediction offers a powerful framework for quantifying uncertainty in machine learning models, enabling the construction of prediction sets with finite-sample validity guarantees. While easily adaptable to non-probabilistic models, applying conformal prediction to probabilistic generative models, such as Normalising Flows is not straightforward. This work proposes a novel method to conformalise conditional normalising flows, specifically addressing the problem of obtaining prediction regions for multi-step time series forecasting. Our approach leverages the flexibility of normalising flows to generate potentially disjoint prediction regions, leading to improved predictive efficiency in the presence of potential multimodal predictive distributions.

JANET: Joint Adaptive predictioN-region Estimation for Time-series

Conformal prediction provides machine learning models with prediction sets that offer theoretical guarantees, but the underlying assumption of exchangeability limits its applicability to time series data. Furthermore, existing approaches struggle to handle multi-step ahead prediction tasks, where uncertainty estimates across multiple future time points are crucial. We propose JANET (Joint Adaptive predictioN-region Estimation for Time-series), a novel framework for constructing conformal prediction regions that are valid for both univariate and multivariate time series. JANET generalises the inductive conformal framework and efficiently produces joint prediction regions with controlled K-familywise error rates, enabling flexible adaptation to specific application needs. Our empirical evaluation demonstrates JANET's superior performance in multi-step prediction tasks across diverse time series datasets, highlighting its potential for reliable and interpretable uncertainty quantification in sequential data.

MixerFlow for Image Modelling

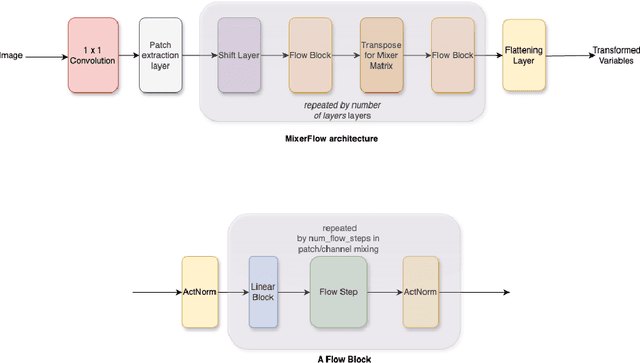
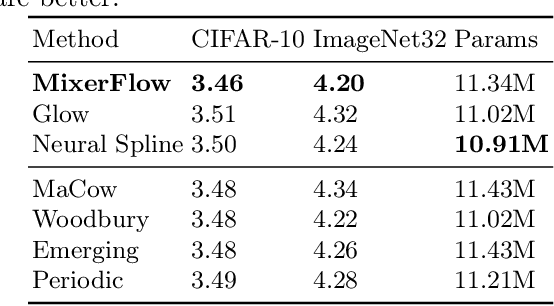
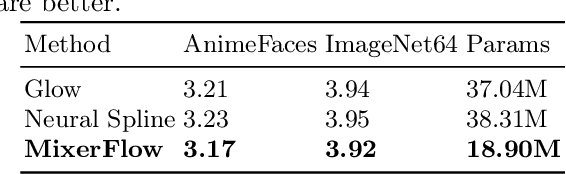
Normalising flows are statistical models that transform a complex density into a simpler density through the use of bijective transformations enabling both density estimation and data generation from a single model. In the context of image modelling, the predominant choice has been the Glow-based architecture, whereas alternative architectures remain largely unexplored in the research community. In this work, we propose a novel architecture called MixerFlow, based on the MLP-Mixer architecture, further unifying the generative and discriminative modelling architectures. MixerFlow offers an effective mechanism for weight sharing for flow-based models. Our results demonstrate better density estimation on image datasets under a fixed computational budget and scales well as the image resolution increases, making MixeFlow a powerful yet simple alternative to the Glow-based architectures. We also show that MixerFlow provides more informative embeddings than Glow-based architectures.

Kernelised Normalising Flows

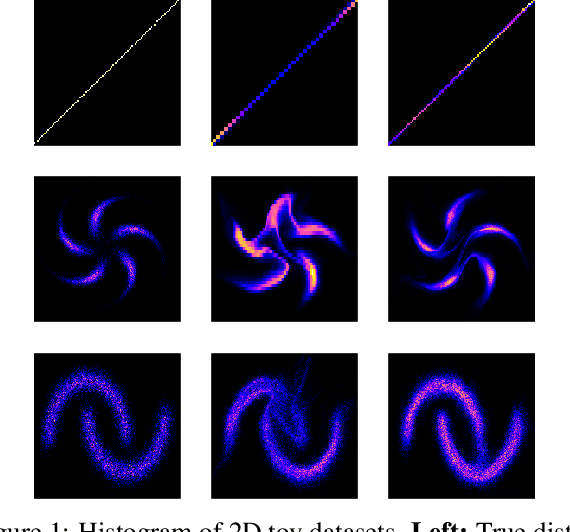
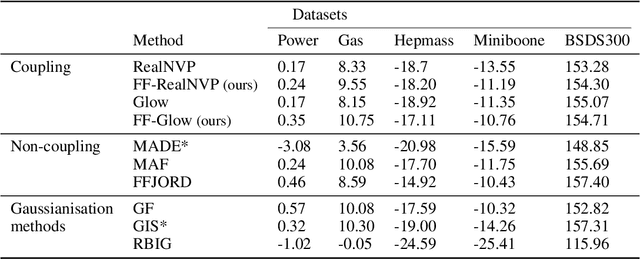
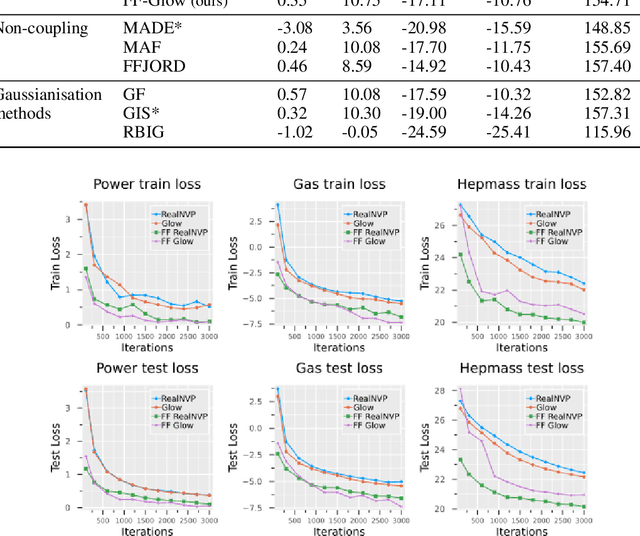
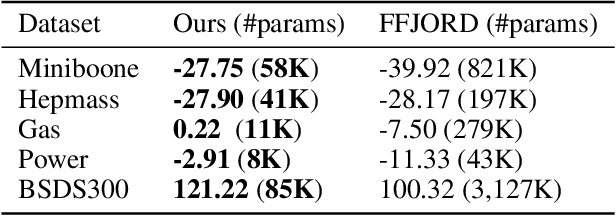
Normalising Flows are generative models characterised by their invertible architecture. However, the requirement of invertibility imposes constraints on their expressiveness, necessitating a large number of parameters and innovative architectural designs to achieve satisfactory outcomes. Whilst flow-based models predominantly rely on neural-network-based transformations for expressive designs, alternative transformation methods have received limited attention. In this work, we present Ferumal flow, a novel kernelised normalising flow paradigm that integrates kernels into the framework. Our results demonstrate that a kernelised flow can yield competitive or superior results compared to neural network-based flows whilst maintaining parameter efficiency. Kernelised flows excel especially in the low-data regime, enabling flexible non-parametric density estimation in applications with sparse data availability.