Interpolation with the polynomial kernels
Paper and Code
Dec 15, 2022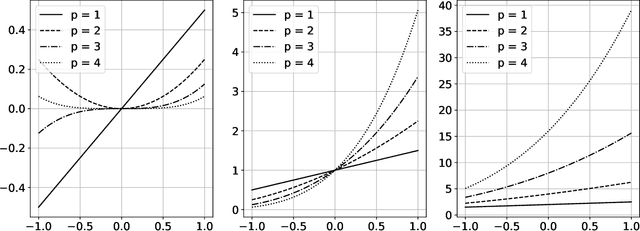
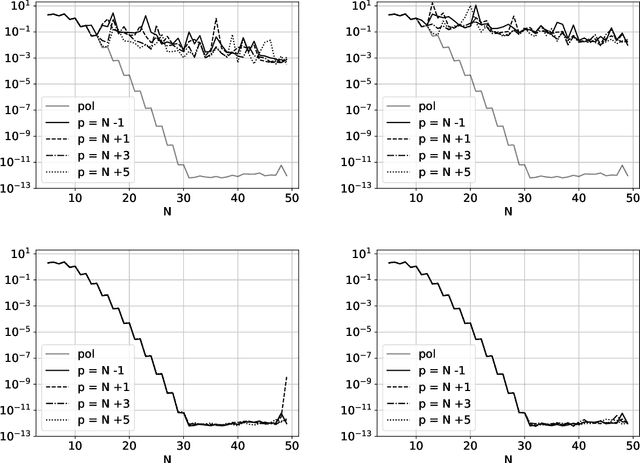
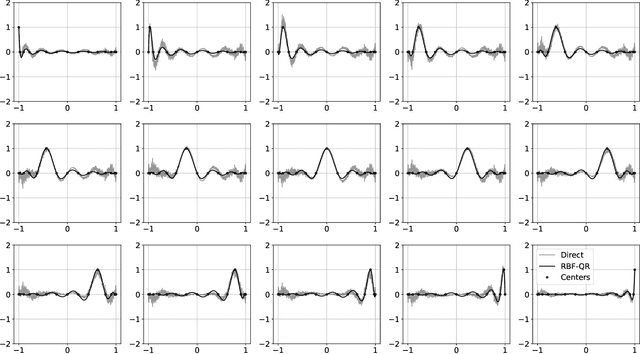
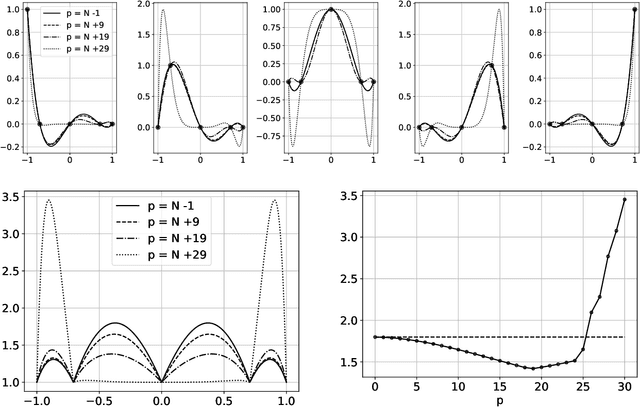
The polynomial kernels are widely used in machine learning and they are one of the default choices to develop kernel-based classification and regression models. However, they are rarely used and considered in numerical analysis due to their lack of strict positive definiteness. In particular they do not enjoy the usual property of unisolvency for arbitrary point sets, which is one of the key properties used to build kernel-based interpolation methods. This paper is devoted to establish some initial results for the study of these kernels, and their related interpolation algorithms, in the context of approximation theory. We will first prove necessary and sufficient conditions on point sets which guarantee the existence and uniqueness of an interpolant. We will then study the Reproducing Kernel Hilbert Spaces (or native spaces) of these kernels and their norms, and provide inclusion relations between spaces corresponding to different kernel parameters. With these spaces at hand, it will be further possible to derive generic error estimates which apply to sufficiently smooth functions, thus escaping the native space. Finally, we will show how to employ an efficient stable algorithm to these kernels to obtain accurate interpolants, and we will test them in some numerical experiment. After this analysis several computational and theoretical aspects remain open, and we will outline possible further research directions in a concluding section. This work builds some bridges between kernel and polynomial interpolation, two topics to which the authors, to different extents, have been introduced under the supervision or through the work of Stefano De Marchi. For this reason, they wish to dedicate this work to him in the occasion of his 60th birthday.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge