Multi-fidelity Hamiltonian Monte Carlo

Numerous applications in biology, statistics, science, and engineering require generating samples from high-dimensional probability distributions. In recent years, the Hamiltonian Monte Carlo (HMC) method has emerged as a state-of-the-art Markov chain Monte Carlo technique, exploiting the shape of such high-dimensional target distributions to efficiently generate samples. Despite its impressive empirical success and increasing popularity, its wide-scale adoption remains limited due to the high computational cost of gradient calculation. Moreover, applying this method is impossible when the gradient of the posterior cannot be computed (for example, with black-box simulators). To overcome these challenges, we propose a novel two-stage Hamiltonian Monte Carlo algorithm with a surrogate model. In this multi-fidelity algorithm, the acceptance probability is computed in the first stage via a standard HMC proposal using an inexpensive differentiable surrogate model, and if the proposal is accepted, the posterior is evaluated in the second stage using the high-fidelity (HF) numerical solver. Splitting the standard HMC algorithm into these two stages allows for approximating the gradient of the posterior efficiently, while producing accurate posterior samples by using HF numerical solvers in the second stage. We demonstrate the effectiveness of this algorithm for a range of problems, including linear and nonlinear Bayesian inverse problems with in-silico data and experimental data. The proposed algorithm is shown to seamlessly integrate with various low-fidelity and HF models, priors, and datasets. Remarkably, our proposed method outperforms the traditional HMC algorithm in both computational and statistical efficiency by several orders of magnitude, all while retaining or improving the accuracy in computed posterior statistics.

Deep learning-based fast solver of the shallow water equations

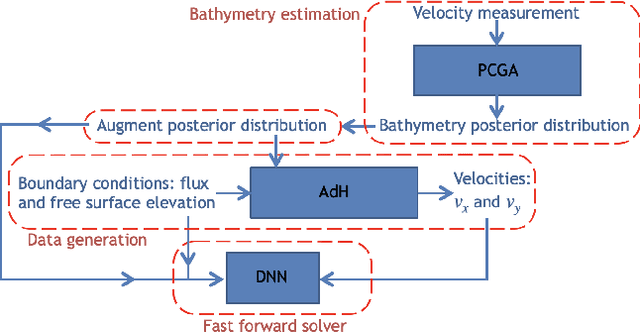
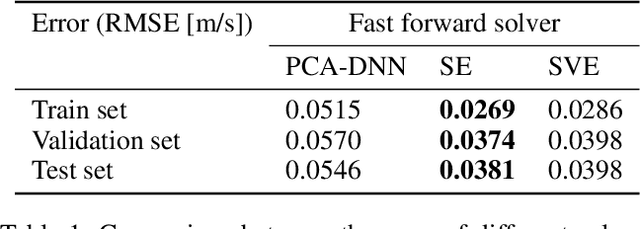
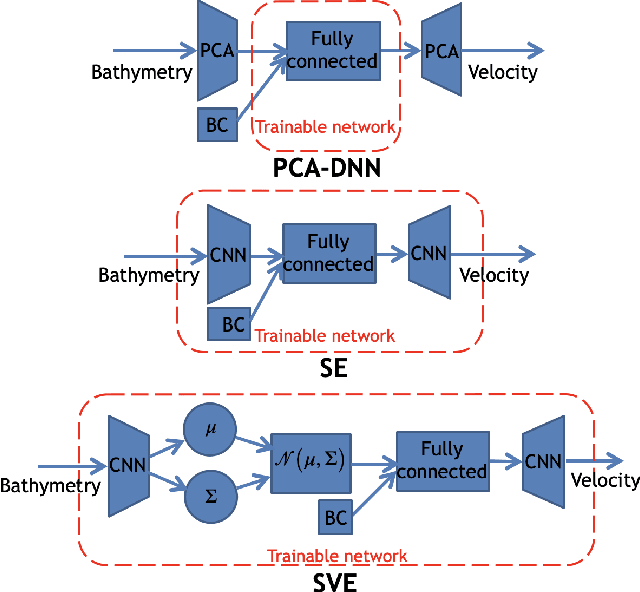
Fast and reliable prediction of river flow velocities is important in many applications, including flood risk management. The shallow water equations (SWEs) are commonly used for this purpose. However, traditional numerical solvers of the SWEs are computationally expensive and require high-resolution riverbed profile measurement (bathymetry). In this work, we propose a two-stage process in which, first, using the principal component geostatistical approach (PCGA) we estimate the probability density function of the bathymetry from flow velocity measurements, and then use machine learning (ML) algorithms to obtain a fast solver for the SWEs. The fast solver uses realizations from the posterior bathymetry distribution and takes as input the prescribed range of BCs. The first stage allows us to predict flow velocities without direct measurement of the bathymetry. Furthermore, we augment the bathymetry posterior distribution to a more general class of distributions before providing them as inputs to ML algorithm in the second stage. This allows the solver to incorporate future direct bathymetry measurements into the flow velocity prediction for improved accuracy, even if the bathymetry changes over time compared to its original indirect estimation. We propose and benchmark three different solvers, referred to as PCA-DNN (principal component analysis-deep neural network), SE (supervised encoder), and SVE (supervised variational encoder), and validate them on the Savannah river, Augusta, GA. Our results show that the fast solvers are capable of predicting flow velocities for different bathymetry and BCs with good accuracy, at a computational cost that is significantly lower than the cost of solving the full boundary value problem with traditional methods.

Data-driven reduced order modeling of environmental hydrodynamics using deep autoencoders and neural ODEs

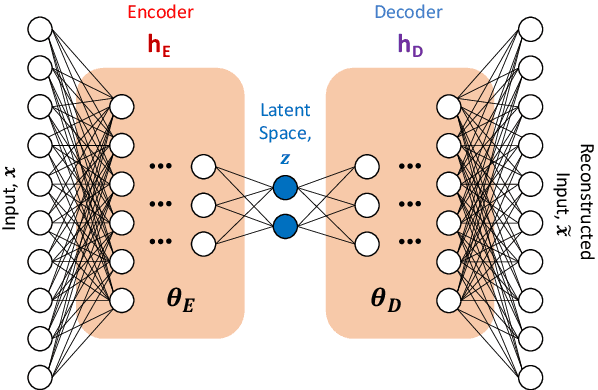
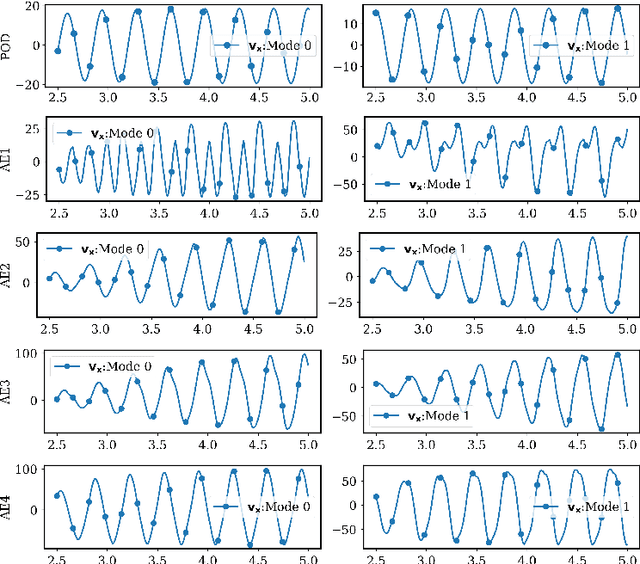
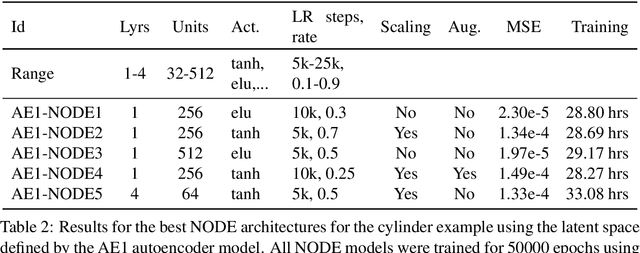
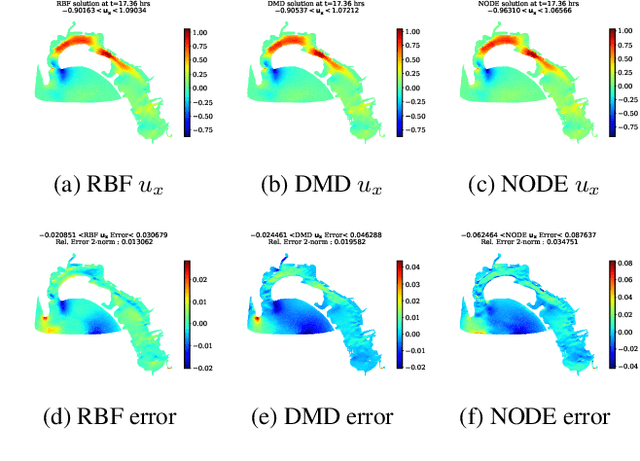
Model reduction for fluid flow simulation continues to be of great interest across a number of scientific and engineering fields. In a previous work [arXiv:2104.13962], we explored the use of Neural Ordinary Differential Equations (NODE) as a non-intrusive method for propagating the latent-space dynamics in reduced order models. Here, we investigate employing deep autoencoders for discovering the reduced basis representation, the dynamics of which are then approximated by NODE. The ability of deep autoencoders to represent the latent-space is compared to the traditional proper orthogonal decomposition (POD) approach, again in conjunction with NODE for capturing the dynamics. Additionally, we compare their behavior with two classical non-intrusive methods based on POD and radial basis function interpolation as well as dynamic mode decomposition. The test problems we consider include incompressible flow around a cylinder as well as a real-world application of shallow water hydrodynamics in an estuarine system. Our findings indicate that deep autoencoders can leverage nonlinear manifold learning to achieve a highly efficient compression of spatial information and define a latent-space that appears to be more suitable for capturing the temporal dynamics through the NODE framework.

Neural Ordinary Differential Equations for Data-Driven Reduced Order Modeling of Environmental Hydrodynamics

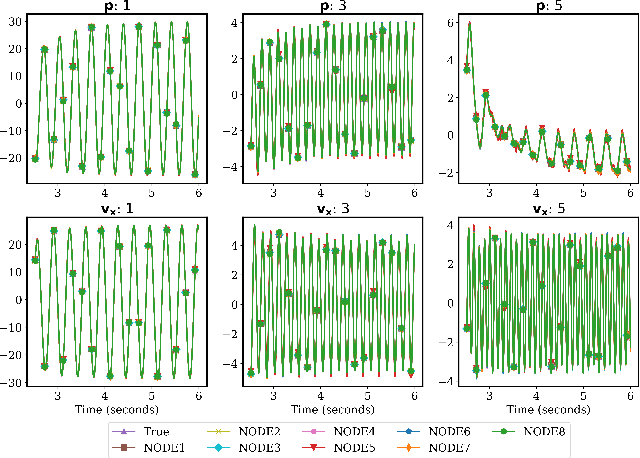
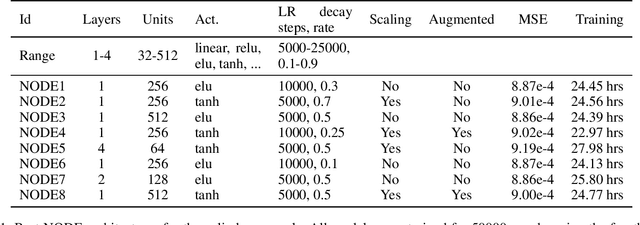
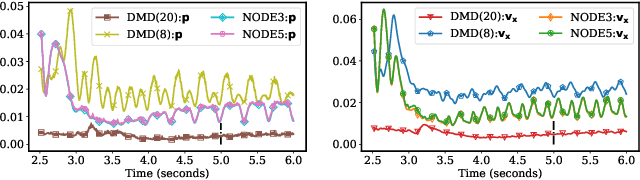
Model reduction for fluid flow simulation continues to be of great interest across a number of scientific and engineering fields. Here, we explore the use of Neural Ordinary Differential Equations, a recently introduced family of continuous-depth, differentiable networks (Chen et al 2018), as a way to propagate latent-space dynamics in reduced order models. We compare their behavior with two classical non-intrusive methods based on proper orthogonal decomposition and radial basis function interpolation as well as dynamic mode decomposition. The test problems we consider include incompressible flow around a cylinder as well as real-world applications of shallow water hydrodynamics in riverine and estuarine systems. Our findings indicate that Neural ODEs provide an elegant framework for stable and accurate evolution of latent-space dynamics with a promising potential of extrapolatory predictions. However, in order to facilitate their widespread adoption for large-scale systems, significant effort needs to be directed at accelerating their training times. This will enable a more comprehensive exploration of the hyperparameter space for building generalizable Neural ODE approximations over a wide range of system dynamics.

Application of deep learning to large scale riverine flow velocity estimation

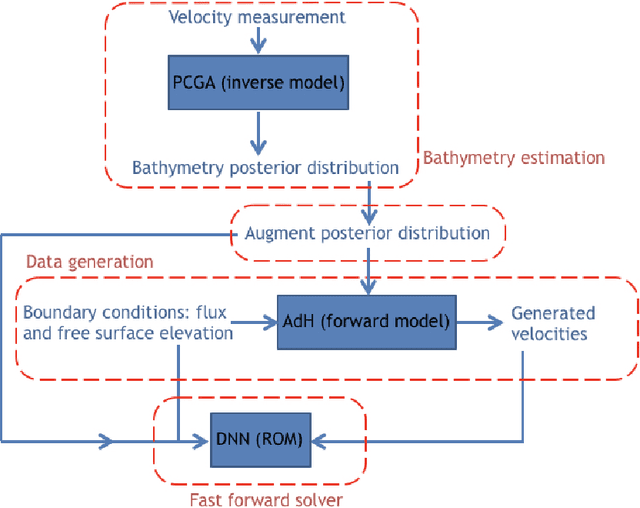
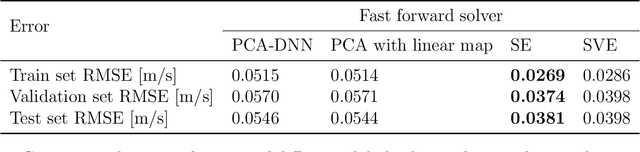
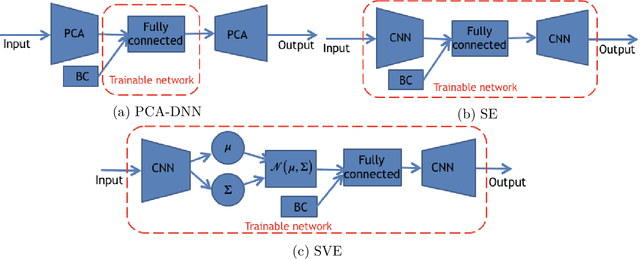
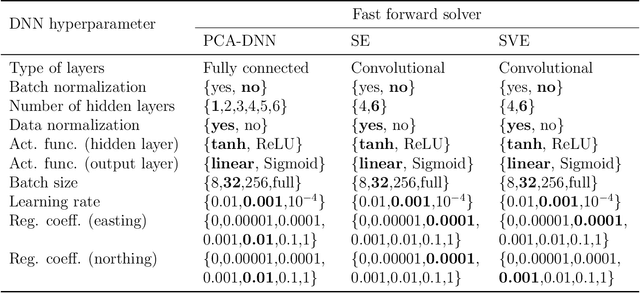
Fast and reliable prediction of riverine flow velocities is important in many applications, including flood risk management. The shallow water equations (SWEs) are commonly used for prediction of the flow velocities. However, accurate and fast prediction with standard SWE solvers is challenging in many cases. Traditional approaches are computationally expensive and require high-resolution riverbed profile measurement ( bathymetry) for accurate predictions. As a result, they are a poor fit in situations where they need to be evaluated repetitively due, for example, to varying boundary condition (BC), or when the bathymetry is not known with certainty. In this work, we propose a two-stage process that tackles these issues. First, using the principal component geostatistical approach (PCGA) we estimate the probability density function of the bathymetry from flow velocity measurements, and then we use multiple machine learning algorithms to obtain a fast solver of the SWEs, given augmented realizations from the posterior bathymetry distribution and the prescribed range of BCs. The first step allows us to predict flow velocities without direct measurement of the bathymetry. Furthermore, the augmentation of the distribution in the second stage allows incorporation of the additional bathymetry information into the flow velocity prediction for improved accuracy and generalization, even if the bathymetry changes over time. Here, we use three solvers, referred to as PCA-DNN (principal component analysis-deep neural network), SE (supervised encoder), and SVE (supervised variational encoder), and validate them on a reach of the Savannah river near Augusta, GA. Our results show that the fast solvers are capable of predicting flow velocities with good accuracy, at a computational cost that is significantly lower than the cost of solving the full boundary value problem with traditional methods.