Physics-based parameterized neural ordinary differential equations: prediction of laser ignition in a rocket combustor

In this work, we present a novel physics-based data-driven framework for reduced-order modeling of laser ignition in a model rocket combustor based on parameterized neural ordinary differential equations (PNODE). Deep neural networks are embedded as functions of high-dimensional parameters of laser ignition to predict various terms in a 0D flow model including the heat source function, pre-exponential factors, and activation energy. Using the governing equations of a 0D flow model, our PNODE needs only a limited number of training samples and predicts trajectories of various quantities such as temperature, pressure, and mass fractions of species while satisfying physical constraints. We validate our physics-based PNODE on solution snapshots of high-fidelity Computational Fluid Dynamics (CFD) simulations of laser-induced ignition in a prototype rocket combustor. We compare the performance of our physics-based PNODE with that of kernel ridge regression and fully connected neural networks. Our results show that our physics-based PNODE provides solutions with lower mean absolute errors of average temperature over time, thus improving the prediction of successful laser ignition with high-dimensional parameters.

Variational encoder geostatistical analysis (VEGAS) with an application to large scale riverine bathymetry

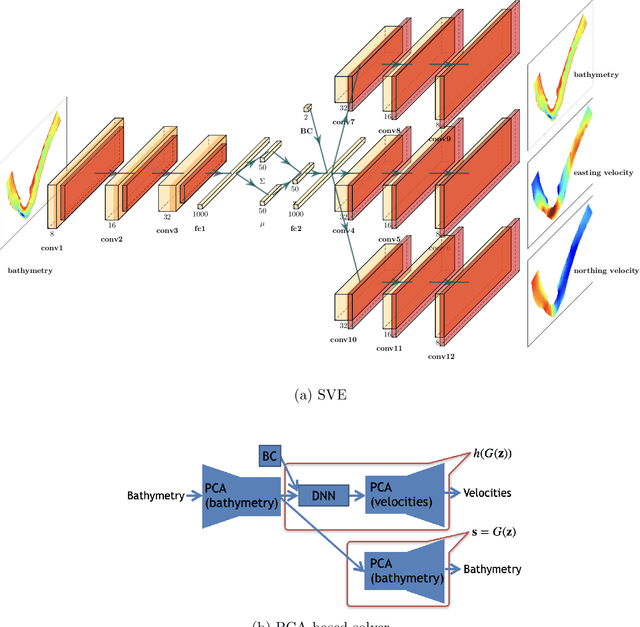
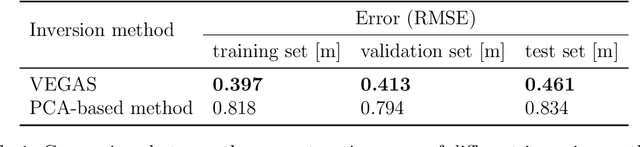
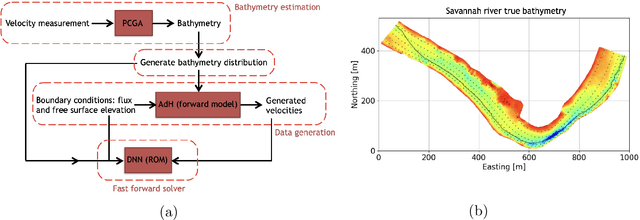
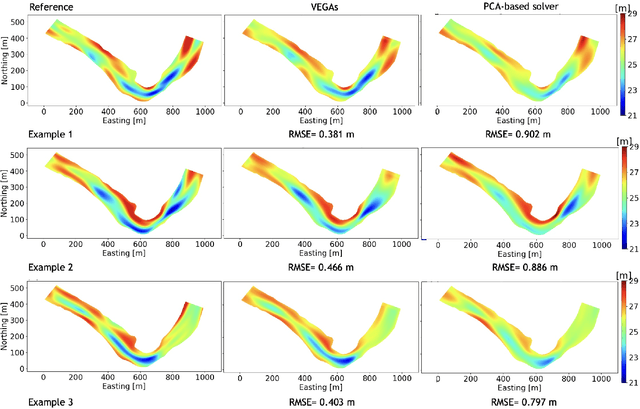
Estimation of riverbed profiles, also known as bathymetry, plays a vital role in many applications, such as safe and efficient inland navigation, prediction of bank erosion, land subsidence, and flood risk management. The high cost and complex logistics of direct bathymetry surveys, i.e., depth imaging, have encouraged the use of indirect measurements such as surface flow velocities. However, estimating high-resolution bathymetry from indirect measurements is an inverse problem that can be computationally challenging. Here, we propose a reduced-order model (ROM) based approach that utilizes a variational autoencoder (VAE), a type of deep neural network with a narrow layer in the middle, to compress bathymetry and flow velocity information and accelerate bathymetry inverse problems from flow velocity measurements. In our application, the shallow-water equations (SWE) with appropriate boundary conditions (BCs), e.g., the discharge and/or the free surface elevation, constitute the forward problem, to predict flow velocity. Then, ROMs of the SWEs are constructed on a nonlinear manifold of low dimensionality through a variational encoder. Estimation with uncertainty quantification (UQ) is performed on the low-dimensional latent space in a Bayesian setting. We have tested our inversion approach on a one-mile reach of the Savannah River, GA, USA. Once the neural network is trained (offline stage), the proposed technique can perform the inversion operation orders of magnitude faster than traditional inversion methods that are commonly based on linear projections, such as principal component analysis (PCA), or the principal component geostatistical approach (PCGA). Furthermore, tests show that the algorithm can estimate the bathymetry with good accuracy even with sparse flow velocity measurements.

Deep learning-based fast solver of the shallow water equations

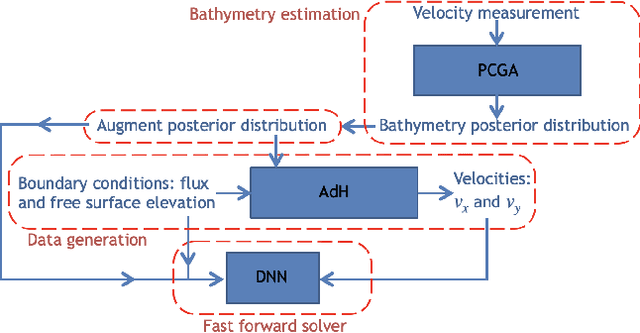
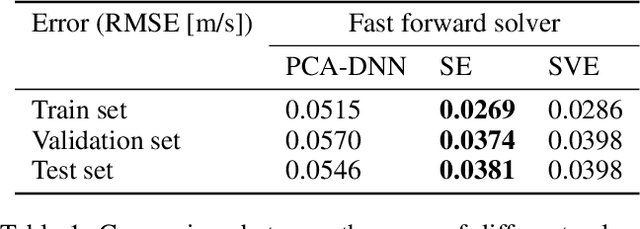
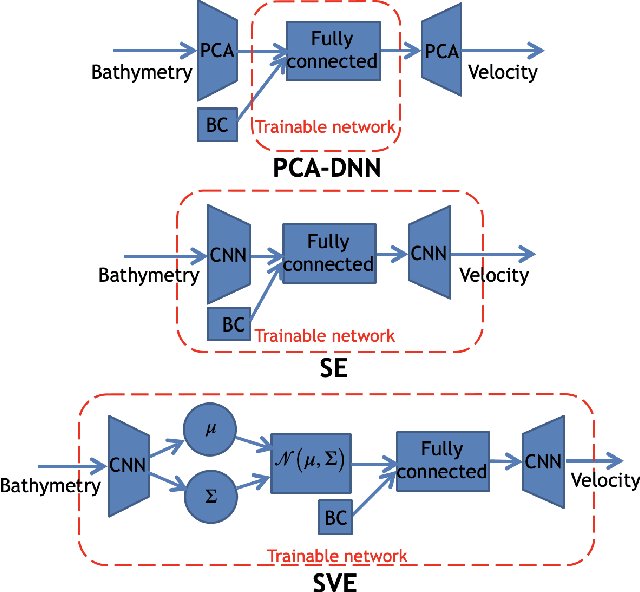
Fast and reliable prediction of river flow velocities is important in many applications, including flood risk management. The shallow water equations (SWEs) are commonly used for this purpose. However, traditional numerical solvers of the SWEs are computationally expensive and require high-resolution riverbed profile measurement (bathymetry). In this work, we propose a two-stage process in which, first, using the principal component geostatistical approach (PCGA) we estimate the probability density function of the bathymetry from flow velocity measurements, and then use machine learning (ML) algorithms to obtain a fast solver for the SWEs. The fast solver uses realizations from the posterior bathymetry distribution and takes as input the prescribed range of BCs. The first stage allows us to predict flow velocities without direct measurement of the bathymetry. Furthermore, we augment the bathymetry posterior distribution to a more general class of distributions before providing them as inputs to ML algorithm in the second stage. This allows the solver to incorporate future direct bathymetry measurements into the flow velocity prediction for improved accuracy, even if the bathymetry changes over time compared to its original indirect estimation. We propose and benchmark three different solvers, referred to as PCA-DNN (principal component analysis-deep neural network), SE (supervised encoder), and SVE (supervised variational encoder), and validate them on the Savannah river, Augusta, GA. Our results show that the fast solvers are capable of predicting flow velocities for different bathymetry and BCs with good accuracy, at a computational cost that is significantly lower than the cost of solving the full boundary value problem with traditional methods.

Application of deep learning to large scale riverine flow velocity estimation

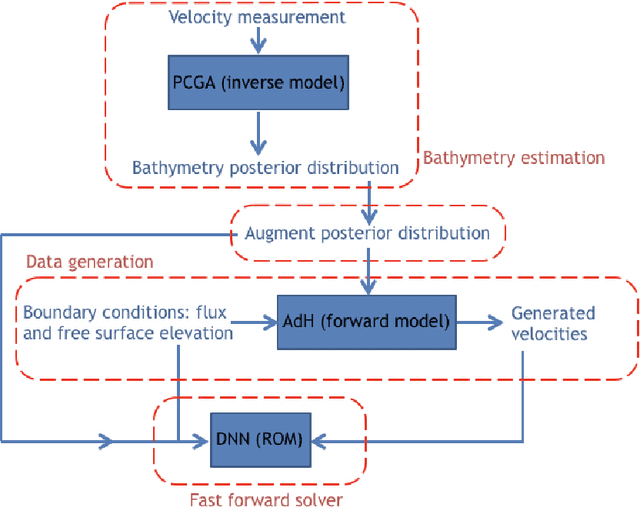
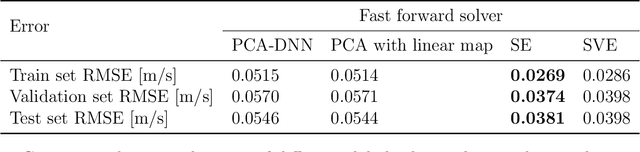
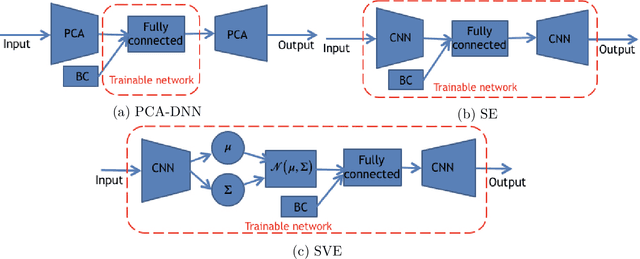
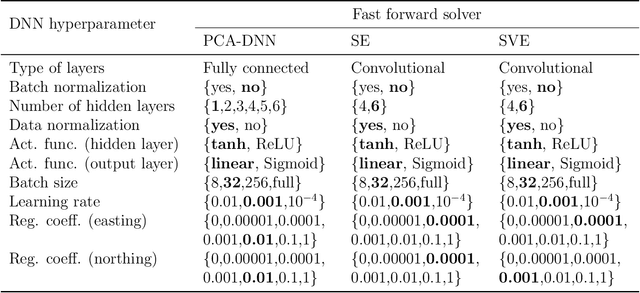
Fast and reliable prediction of riverine flow velocities is important in many applications, including flood risk management. The shallow water equations (SWEs) are commonly used for prediction of the flow velocities. However, accurate and fast prediction with standard SWE solvers is challenging in many cases. Traditional approaches are computationally expensive and require high-resolution riverbed profile measurement ( bathymetry) for accurate predictions. As a result, they are a poor fit in situations where they need to be evaluated repetitively due, for example, to varying boundary condition (BC), or when the bathymetry is not known with certainty. In this work, we propose a two-stage process that tackles these issues. First, using the principal component geostatistical approach (PCGA) we estimate the probability density function of the bathymetry from flow velocity measurements, and then we use multiple machine learning algorithms to obtain a fast solver of the SWEs, given augmented realizations from the posterior bathymetry distribution and the prescribed range of BCs. The first step allows us to predict flow velocities without direct measurement of the bathymetry. Furthermore, the augmentation of the distribution in the second stage allows incorporation of the additional bathymetry information into the flow velocity prediction for improved accuracy and generalization, even if the bathymetry changes over time. Here, we use three solvers, referred to as PCA-DNN (principal component analysis-deep neural network), SE (supervised encoder), and SVE (supervised variational encoder), and validate them on a reach of the Savannah river near Augusta, GA. Our results show that the fast solvers are capable of predicting flow velocities with good accuracy, at a computational cost that is significantly lower than the cost of solving the full boundary value problem with traditional methods.

Application of Deep Learning-based Interpolation Methods to Nearshore Bathymetry

Nearshore bathymetry, the topography of the ocean floor in coastal zones, is vital for predicting the surf zone hydrodynamics and for route planning to avoid subsurface features. Hence, it is increasingly important for a wide variety of applications, including shipping operations, coastal management, and risk assessment. However, direct high resolution surveys of nearshore bathymetry are rarely performed due to budget constraints and logistical restrictions. Another option when only sparse observations are available is to use Gaussian Process regression (GPR), also called Kriging. But GPR has difficulties recognizing patterns with sharp gradients, like those found around sand bars and submerged objects, especially when observations are sparse. In this work, we present several deep learning-based techniques to estimate nearshore bathymetry with sparse, multi-scale measurements. We propose a Deep Neural Network (DNN) to compute posterior estimates of the nearshore bathymetry, as well as a conditional Generative Adversarial Network (cGAN) that samples from the posterior distribution. We train our neural networks based on synthetic data generated from nearshore surveys provided by the U.S.\ Army Corps of Engineer Field Research Facility (FRF) in Duck, North Carolina. We compare our methods with Kriging on real surveys as well as surveys with artificially added sharp gradients. Results show that direct estimation by DNN gives better predictions than Kriging in this application. We use bootstrapping with DNN for uncertainty quantification. We also propose a method, named DNN-Kriging, that combines deep learning with Kriging and shows further improvement of the posterior estimates.