Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

Variational encoder geostatistical analysis (VEGAS) with an application to large scale riverine bathymetry

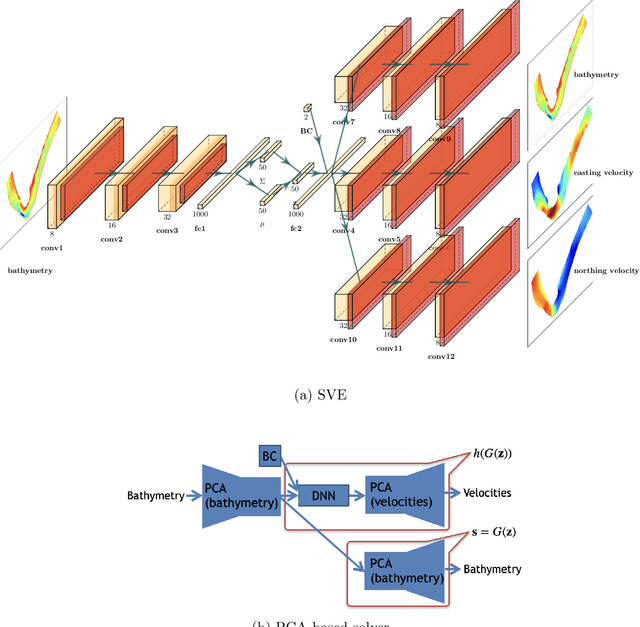
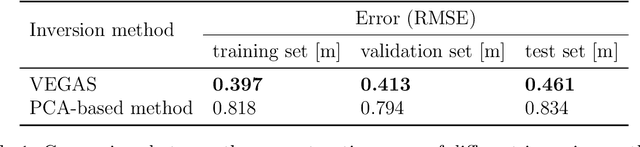
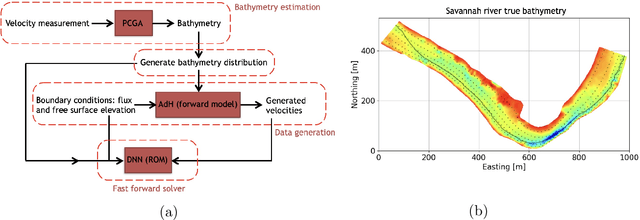
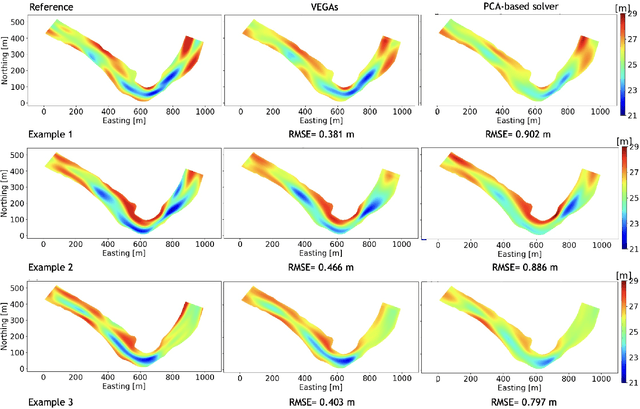
Estimation of riverbed profiles, also known as bathymetry, plays a vital role in many applications, such as safe and efficient inland navigation, prediction of bank erosion, land subsidence, and flood risk management. The high cost and complex logistics of direct bathymetry surveys, i.e., depth imaging, have encouraged the use of indirect measurements such as surface flow velocities. However, estimating high-resolution bathymetry from indirect measurements is an inverse problem that can be computationally challenging. Here, we propose a reduced-order model (ROM) based approach that utilizes a variational autoencoder (VAE), a type of deep neural network with a narrow layer in the middle, to compress bathymetry and flow velocity information and accelerate bathymetry inverse problems from flow velocity measurements. In our application, the shallow-water equations (SWE) with appropriate boundary conditions (BCs), e.g., the discharge and/or the free surface elevation, constitute the forward problem, to predict flow velocity. Then, ROMs of the SWEs are constructed on a nonlinear manifold of low dimensionality through a variational encoder. Estimation with uncertainty quantification (UQ) is performed on the low-dimensional latent space in a Bayesian setting. We have tested our inversion approach on a one-mile reach of the Savannah River, GA, USA. Once the neural network is trained (offline stage), the proposed technique can perform the inversion operation orders of magnitude faster than traditional inversion methods that are commonly based on linear projections, such as principal component analysis (PCA), or the principal component geostatistical approach (PCGA). Furthermore, tests show that the algorithm can estimate the bathymetry with good accuracy even with sparse flow velocity measurements.

Application of Deep Learning-based Interpolation Methods to Nearshore Bathymetry

Nearshore bathymetry, the topography of the ocean floor in coastal zones, is vital for predicting the surf zone hydrodynamics and for route planning to avoid subsurface features. Hence, it is increasingly important for a wide variety of applications, including shipping operations, coastal management, and risk assessment. However, direct high resolution surveys of nearshore bathymetry are rarely performed due to budget constraints and logistical restrictions. Another option when only sparse observations are available is to use Gaussian Process regression (GPR), also called Kriging. But GPR has difficulties recognizing patterns with sharp gradients, like those found around sand bars and submerged objects, especially when observations are sparse. In this work, we present several deep learning-based techniques to estimate nearshore bathymetry with sparse, multi-scale measurements. We propose a Deep Neural Network (DNN) to compute posterior estimates of the nearshore bathymetry, as well as a conditional Generative Adversarial Network (cGAN) that samples from the posterior distribution. We train our neural networks based on synthetic data generated from nearshore surveys provided by the U.S.\ Army Corps of Engineer Field Research Facility (FRF) in Duck, North Carolina. We compare our methods with Kriging on real surveys as well as surveys with artificially added sharp gradients. Results show that direct estimation by DNN gives better predictions than Kriging in this application. We use bootstrapping with DNN for uncertainty quantification. We also propose a method, named DNN-Kriging, that combines deep learning with Kriging and shows further improvement of the posterior estimates.