A Neural Operator-Based Emulator for Regional Shallow Water Dynamics

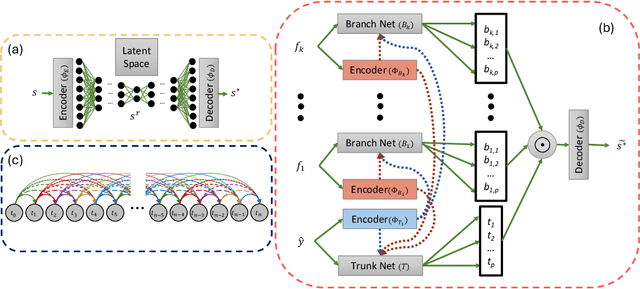
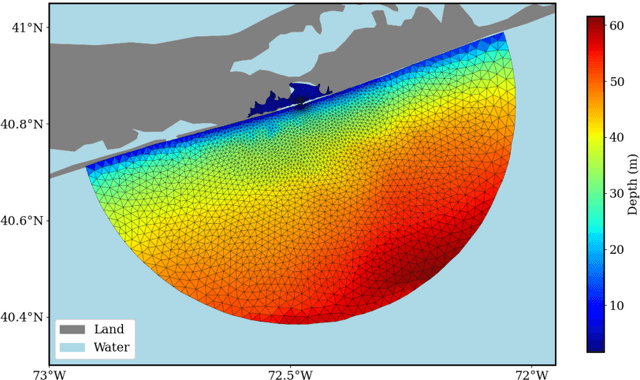
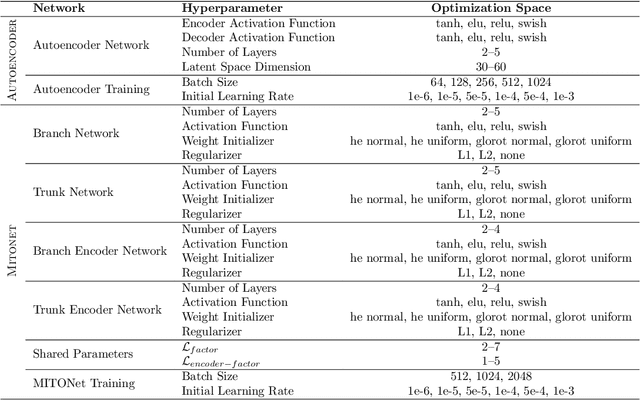
Coastal regions are particularly vulnerable to the impacts of rising sea levels and extreme weather events. Accurate real-time forecasting of hydrodynamic processes in these areas is essential for infrastructure planning and climate adaptation. In this study, we present the Multiple-Input Temporal Operator Network (MITONet), a novel autoregressive neural emulator that employs dimensionality reduction to efficiently approximate high-dimensional numerical solvers for complex, nonlinear problems that are governed by time-dependent, parameterized partial differential equations. Although MITONet is applicable to a wide range of problems, we showcase its capabilities by forecasting regional tide-driven dynamics described by the two-dimensional shallow-water equations, while incorporating initial conditions, boundary conditions, and a varying domain parameter. We demonstrate MITONet's performance in a real-world application, highlighting its ability to make accurate predictions by extrapolating both in time and parametric space.

Topological derivative approach for deep neural network architecture adaptation

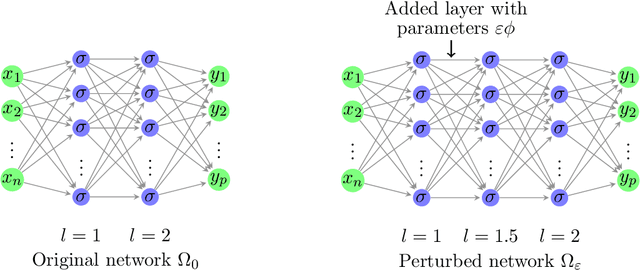
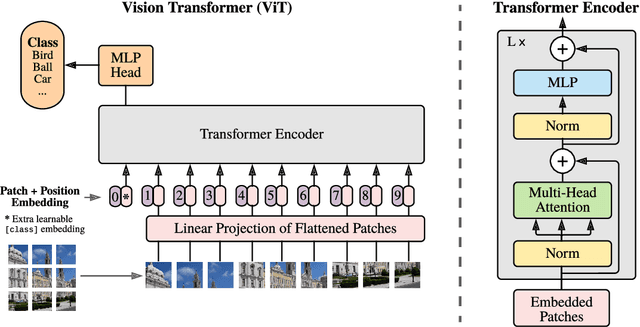
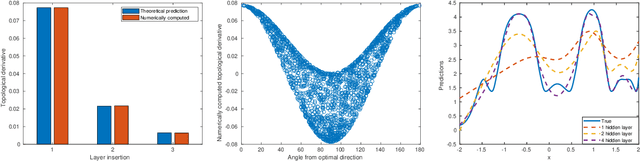
This work presents a novel algorithm for progressively adapting neural network architecture along the depth. In particular, we attempt to address the following questions in a mathematically principled way: i) Where to add a new capacity (layer) during the training process? ii) How to initialize the new capacity? At the heart of our approach are two key ingredients: i) the introduction of a ``shape functional" to be minimized, which depends on neural network topology, and ii) the introduction of a topological derivative of the shape functional with respect to the neural network topology. Using an optimal control viewpoint, we show that the network topological derivative exists under certain conditions, and its closed-form expression is derived. In particular, we explore, for the first time, the connection between the topological derivative from a topology optimization framework with the Hamiltonian from optimal control theory. Further, we show that the optimality condition for the shape functional leads to an eigenvalue problem for deep neural architecture adaptation. Our approach thus determines the most sensitive location along the depth where a new layer needs to be inserted during the training phase and the associated parametric initialization for the newly added layer. We also demonstrate that our layer insertion strategy can be derived from an optimal transport viewpoint as a solution to maximizing a topological derivative in $p$-Wasserstein space, where $p>= 1$. Numerical investigations with fully connected network, convolutional neural network, and vision transformer on various regression and classification problems demonstrate that our proposed approach can outperform an ad-hoc baseline network and other architecture adaptation strategies. Further, we also demonstrate other applications of topological derivative in fields such as transfer learning.

Storm Surge Modeling in the AI ERA: Using LSTM-based Machine Learning for Enhancing Forecasting Accuracy

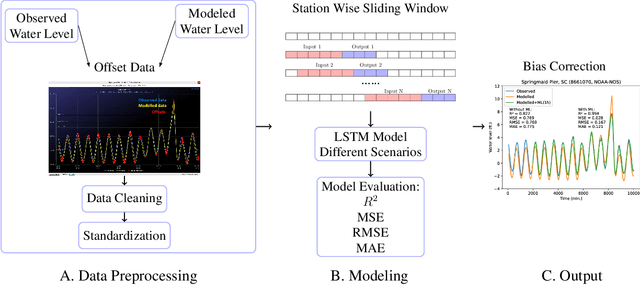
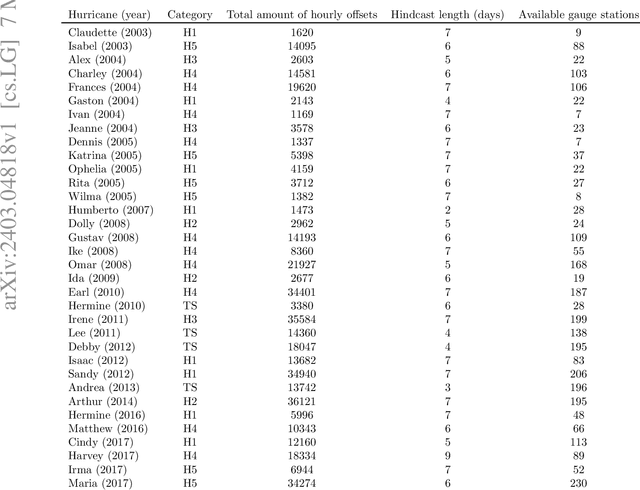
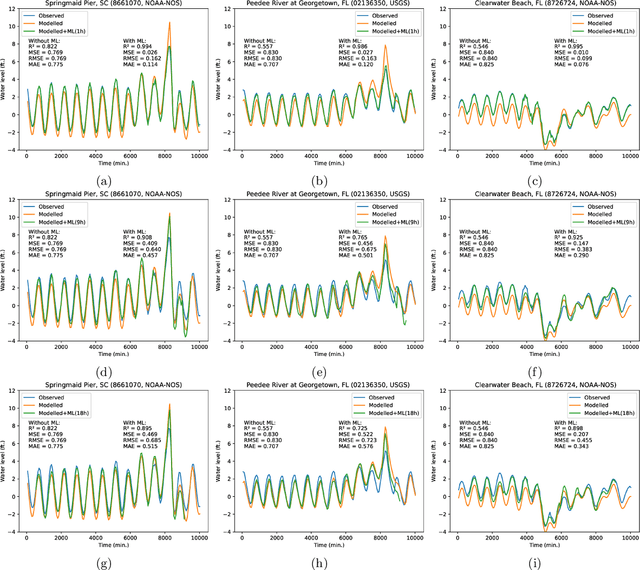
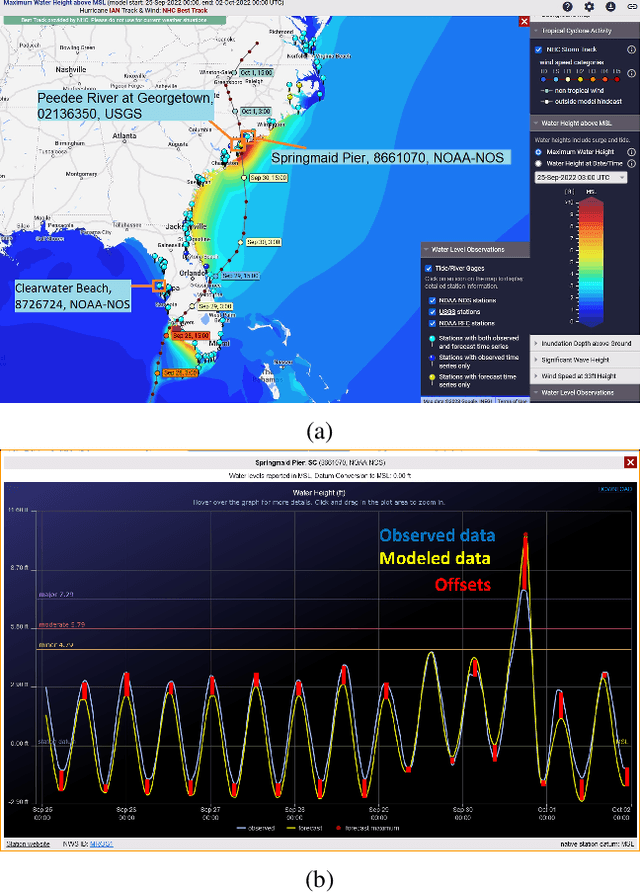
Physics simulation results of natural processes usually do not fully capture the real world. This is caused for instance by limits in what physical processes are simulated and to what accuracy. In this work we propose and analyze the use of an LSTM-based deep learning network machine learning (ML) architecture for capturing and predicting the behavior of the systemic error for storm surge forecast models with respect to real-world water height observations from gauge stations during hurricane events. The overall goal of this work is to predict the systemic error of the physics model and use it to improve the accuracy of the simulation results post factum. We trained our proposed ML model on a dataset of 61 historical storms in the coastal regions of the U.S. and we tested its performance in bias correcting modeled water level data predictions from hurricane Ian (2022). We show that our model can consistently improve the forecasting accuracy for hurricane Ian -- unknown to the ML model -- at all gauge station coordinates used for the initial data. Moreover, by examining the impact of using different subsets of the initial training dataset, containing a number of relatively similar or different hurricanes in terms of hurricane track, we found that we can obtain similar quality of bias correction by only using a subset of six hurricanes. This is an important result that implies the possibility to apply a pre-trained ML model to real-time hurricane forecasting results with the goal of bias correcting and improving the produced simulation accuracy. The presented work is an important first step in creating a bias correction system for real-time storm surge forecasting applicable to the full simulation area. It also presents a highly transferable and operationally applicable methodology for improving the accuracy in a wide range of physics simulation scenarios beyond storm surge forecasting.

Rapid Flood Inundation Forecast Using Fourier Neural Operator

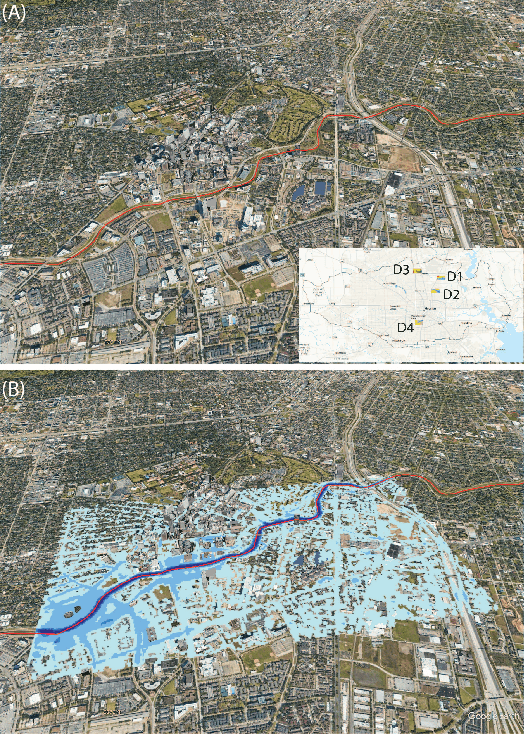
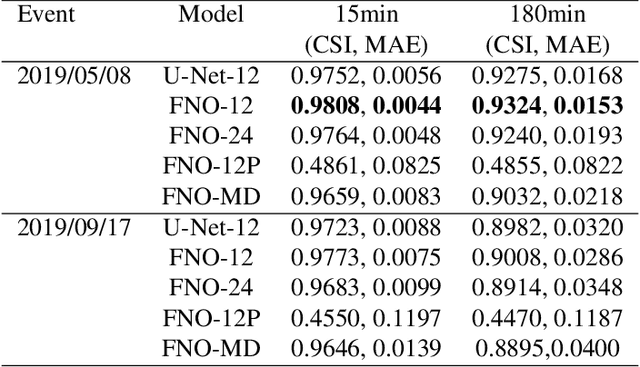
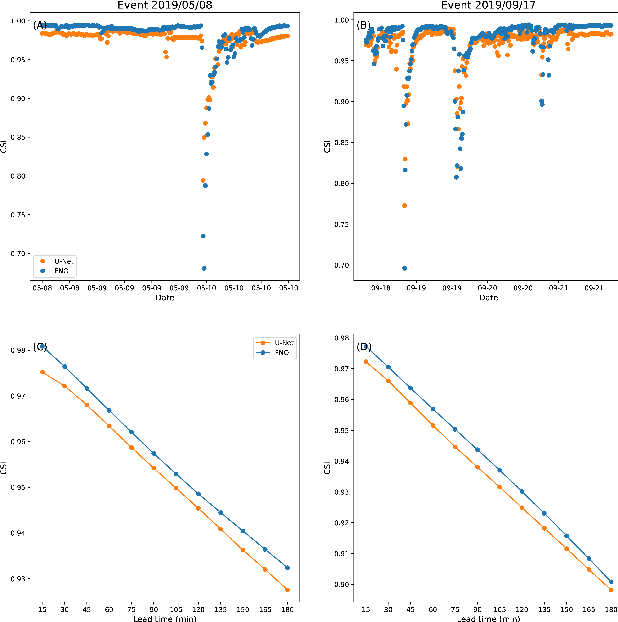
Flood inundation forecast provides critical information for emergency planning before and during flood events. Real time flood inundation forecast tools are still lacking. High-resolution hydrodynamic modeling has become more accessible in recent years, however, predicting flood extents at the street and building levels in real-time is still computationally demanding. Here we present a hybrid process-based and data-driven machine learning (ML) approach for flood extent and inundation depth prediction. We used the Fourier neural operator (FNO), a highly efficient ML method, for surrogate modeling. The FNO model is demonstrated over an urban area in Houston (Texas, U.S.) by training using simulated water depths (in 15-min intervals) from six historical storm events and then tested over two holdout events. Results show FNO outperforms the baseline U-Net model. It maintains high predictability at all lead times tested (up to 3 hrs) and performs well when applying to new sites, suggesting strong generalization skill.

Learning Storm Surge with Gradient Boosting

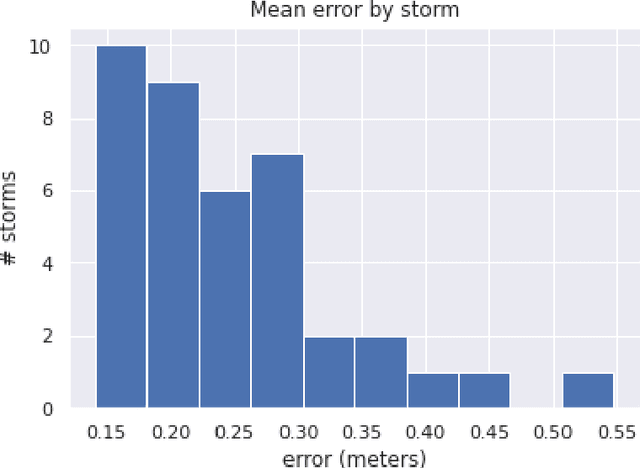
Storm surge is a major natural hazard for coastal regions, responsible both for significant property damage and loss of life. Accurate, efficient models of storm surge are needed both to assess long-term risk and to guide emergency management decisions. While high-fidelity ocean circulation models such as the ADvanced CIRCulation (ADCIRC) model can accurately predict storm surge, they are very computationally expensive. Consequently, there have been a number of efforts in recent years to develop data-driven surrogate models for storm surge. While these models can attain good accuracy and are highly efficient, they are often limited to a small geographical region and a fixed set of output locations. We develop a novel surrogate model for peak storm surge prediction based on gradient boosting. Unlike most surrogate approaches, our model is not explicitly constrained to a fixed set of output locations or specific geographical region. The model is trained with a database of 446 synthetic storms that make landfall on the Texas coast and obtains a mean absolute error of 0.25 meters. We additionally present a test of the model on Hurricanes Ike (2008) and Harvey (2017).

SCA-Net: A Self-Correcting Two-Layer Autoencoder for Hyper-spectral Unmixing

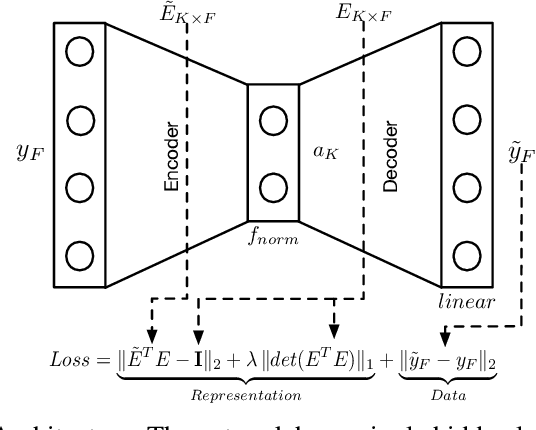
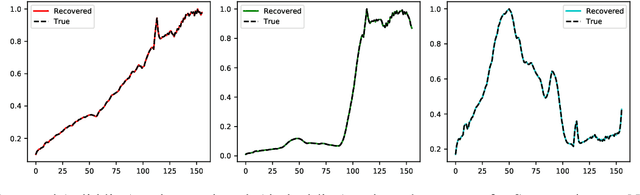
Linear Mixture Model for hyperspectral datasets involves separating a mixed pixel as a linear combination of its constituent endmembers and corresponding fractional abundances. Both optimization and neural methods have attempted to tackle this problem, with the current state of the art results achieved by neural models on benchmark datasets. However, our review of these neural models show that these networks are severely over-parameterized and consequently the invariant endmember spectra extracted as decoder weights has a high variance over multiple runs. All of these approaches require substantial post-processing to satisfy LMM constraints. Furthermore, they also require an exact specification of the number of endmembers and specialized initialization of weights from other algorithms like VCA. Our work shows for the first time that a two-layer autoencoder (SCA-Net), with $2FK$ parameters ($F$ features, $K$ endmembers), achieves error metrics that are scales apart ($10^{-5})$ from previously reported values $(10^{-2})$. SCA-Net converges to this low error solution starting from a random initialization of weights. We also show that SCA-Net, based upon a bi-orthogonal representation, performs a self-correction when the the number of endmembers are over-specified. We show that our network formulation extracts a low-rank representation that is bounded below by a tail-energy and can be computationally verified. Our numerical experiments on Samson, Jasper, and Urban datasets demonstrate that SCA-Net outperforms previously reported error metrics for all the cases while being robust to noise and outliers.

A Hybrid 2-stage Neural Optimization for Pareto Front Extraction

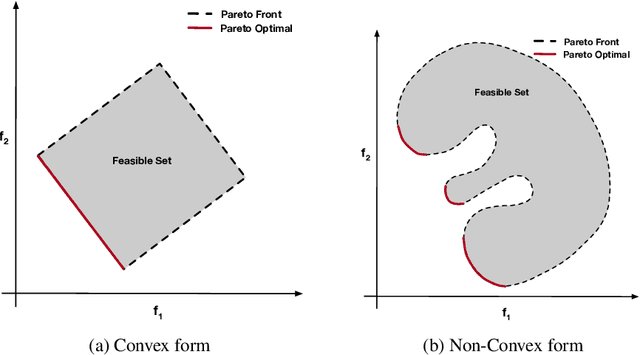
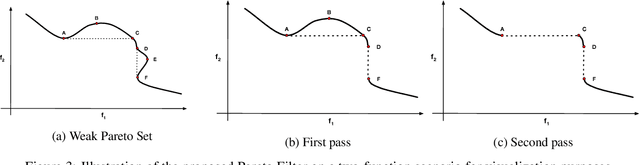
Classification, recommendation, and ranking problems often involve competing goals with additional constraints (e.g., to satisfy fairness or diversity criteria). Such optimization problems are quite challenging, often involving non-convex functions along with considerations of user preferences in balancing trade-offs. Pareto solutions represent optimal frontiers for jointly optimizing multiple competing objectives. A major obstacle for frequently used linear-scalarization strategies is that the resulting optimization problem might not always converge to a global optimum. Furthermore, such methods only return one solution point per run. A Pareto solution set is a subset of all such global optima over multiple runs for different trade-off choices. Therefore, a Pareto front can only be guaranteed with multiple runs of the linear-scalarization problem, where all runs converge to their respective global optima. Consequently, extracting a Pareto front for practical problems is computationally intractable with substantial computational overheads, limited scalability, and reduced accuracy. We propose a robust, low cost, two-stage, hybrid neural Pareto optimization approach that is accurate and scales (compute space and time) with data dimensions, as well as number of functions and constraints. The first stage (neural network) efficiently extracts a weak Pareto front, using Fritz-John conditions as the discriminator, with no assumptions of convexity on the objectives or constraints. The second stage (efficient Pareto filter) extracts the strong Pareto optimal subset given the weak front from stage 1. Fritz-John conditions provide us with theoretical bounds on approximation error between the true and network extracted weak Pareto front. Numerical experiments demonstrates the accuracy and efficiency on a canonical set of benchmark problems and a fairness optimization task from prior works.

Streaming Singular Value Decomposition for Big Data Applications

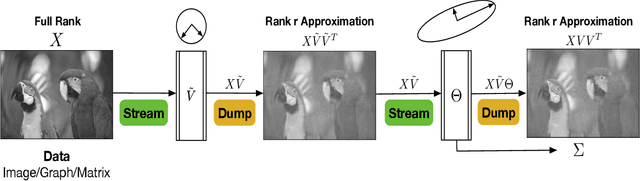
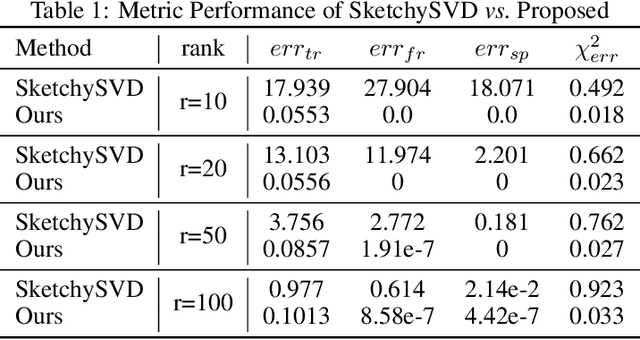
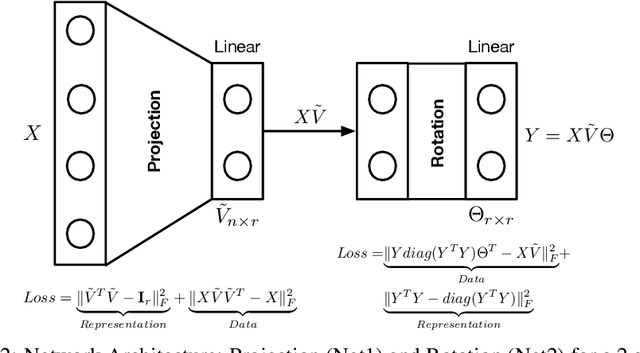
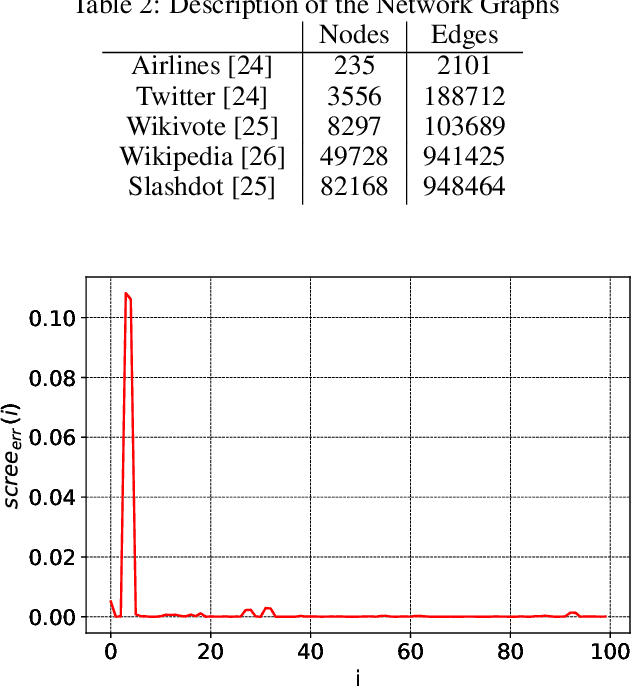
Singular Value Decomposition (SVD) plays a pivotal role in exploratory data analysis. However, in a Big Data setting computing the dominant singular vectors is often restrictive due to the main memory requirements imposed by the dataset. Recently introduced randomized projection schemes attempt to mitigate this memory load by constructing approximate projections of the true dataset in a streaming setting. However, these projection methods come at the cost of approximation errors in both top singular values and vectors. Furthermore, in order to bound the approximation error, an over-sampled projection is required, often much larger in dimension than the desired rank. This latter consideration can still be memory intensive when the data dimension is large or extraneous when the desired rank approximation is close to the full rank. We present a two stage neural optimization approach as an alternative to conventional and randomized SVD techniques, where the memory requirement depends explicitly on the feature dimension and desired rank, independent of the sample size. The proposed scheme reads data samples in a streaming setting with the network minimization problem converging to a low rank approximation with high precision. Our architecture is fully interpretable where all the network outputs and weights have a specific meaning. We evaluate our results on various performance metrics against state of the art streaming methods. We also present numerical experiments for Singular and Eigen value decomposition on real data at various scales to show the memory efficiency of our proposed approach.