Sentinel: Dynamic Knowledge Distillation for Personalized Federated Intrusion Detection in Heterogeneous IoT Networks

Federated learning (FL) offers a privacy-preserving paradigm for machine learning, but its application in intrusion detection systems (IDS) within IoT networks is challenged by severe class imbalance, non-IID data, and high communication overhead.These challenges severely degrade the performance of conventional FL methods in real-world network traffic classification. To overcome these limitations, we propose Sentinel, a personalized federated IDS (pFed-IDS) framework that incorporates a dual-model architecture on each client, consisting of a personalized teacher and a lightweight shared student model. This design effectively balances deep local adaptation with efficient global model consensus while preserving client privacy by transmitting only the compact student model, thus reducing communication costs. Sentinel integrates three key mechanisms to ensure robust performance: bidirectional knowledge distillation with adaptive temperature scaling, multi-faceted feature alignment, and class-balanced loss functions. Furthermore, the server employs normalized gradient aggregation with equal client weighting to enhance fairness and mitigate client drift. Extensive experiments on the IoTID20 and 5GNIDD benchmark datasets demonstrate that Sentinel significantly outperforms state-of-the-art federated methods, establishing a new performance benchmark, especially under extreme data heterogeneity, while maintaining communication efficiency.

A Comprehensive Dataset for Human vs. AI Generated Text Detection

The rapid advancement of large language models (LLMs) has led to increasingly human-like AI-generated text, raising concerns about content authenticity, misinformation, and trustworthiness. Addressing the challenge of reliably detecting AI-generated text and attributing it to specific models requires large-scale, diverse, and well-annotated datasets. In this work, we present a comprehensive dataset comprising over 58,000 text samples that combine authentic New York Times articles with synthetic versions generated by multiple state-of-the-art LLMs including Gemma-2-9b, Mistral-7B, Qwen-2-72B, LLaMA-8B, Yi-Large, and GPT-4-o. The dataset provides original article abstracts as prompts, full human-authored narratives. We establish baseline results for two key tasks: distinguishing human-written from AI-generated text, achieving an accuracy of 58.35\%, and attributing AI texts to their generating models with an accuracy of 8.92\%. By bridging real-world journalistic content with modern generative models, the dataset aims to catalyze the development of robust detection and attribution methods, fostering trust and transparency in the era of generative AI. Our dataset is available at: https://huggingface.co/datasets/gsingh1-py/train.

DETONATE: A Benchmark for Text-to-Image Alignment and Kernelized Direct Preference Optimization

Alignment is crucial for text-to-image (T2I) models to ensure that generated images faithfully capture user intent while maintaining safety and fairness. Direct Preference Optimization (DPO), prominent in large language models (LLMs), is extending its influence to T2I systems. This paper introduces DPO-Kernels for T2I models, a novel extension enhancing alignment across three dimensions: (i) Hybrid Loss, integrating embedding-based objectives with traditional probability-based loss for improved optimization; (ii) Kernelized Representations, employing Radial Basis Function (RBF), Polynomial, and Wavelet kernels for richer feature transformations and better separation between safe and unsafe inputs; and (iii) Divergence Selection, expanding beyond DPO's default Kullback-Leibler (KL) regularizer by incorporating Wasserstein and R'enyi divergences for enhanced stability and robustness. We introduce DETONATE, the first large-scale benchmark of its kind, comprising approximately 100K curated image pairs categorized as chosen and rejected. DETONATE encapsulates three axes of social bias and discrimination: Race, Gender, and Disability. Prompts are sourced from hate speech datasets, with images generated by leading T2I models including Stable Diffusion 3.5 Large, Stable Diffusion XL, and Midjourney. Additionally, we propose the Alignment Quality Index (AQI), a novel geometric measure quantifying latent-space separability of safe/unsafe image activations, revealing hidden vulnerabilities. Empirically, we demonstrate that DPO-Kernels maintain strong generalization bounds via Heavy-Tailed Self-Regularization (HT-SR). DETONATE and complete code are publicly released.

YINYANG-ALIGN: Benchmarking Contradictory Objectives and Proposing Multi-Objective Optimization based DPO for Text-to-Image Alignment

Precise alignment in Text-to-Image (T2I) systems is crucial to ensure that generated visuals not only accurately encapsulate user intents but also conform to stringent ethical and aesthetic benchmarks. Incidents like the Google Gemini fiasco, where misaligned outputs triggered significant public backlash, underscore the critical need for robust alignment mechanisms. In contrast, Large Language Models (LLMs) have achieved notable success in alignment. Building on these advancements, researchers are eager to apply similar alignment techniques, such as Direct Preference Optimization (DPO), to T2I systems to enhance image generation fidelity and reliability. We present YinYangAlign, an advanced benchmarking framework that systematically quantifies the alignment fidelity of T2I systems, addressing six fundamental and inherently contradictory design objectives. Each pair represents fundamental tensions in image generation, such as balancing adherence to user prompts with creative modifications or maintaining diversity alongside visual coherence. YinYangAlign includes detailed axiom datasets featuring human prompts, aligned (chosen) responses, misaligned (rejected) AI-generated outputs, and explanations of the underlying contradictions.

DPO Kernels: A Semantically-Aware, Kernel-Enhanced, and Divergence-Rich Paradigm for Direct Preference Optimization

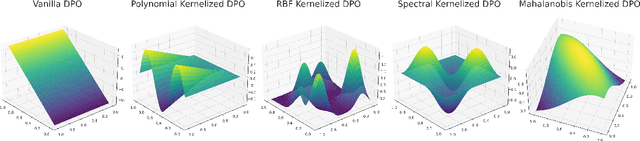
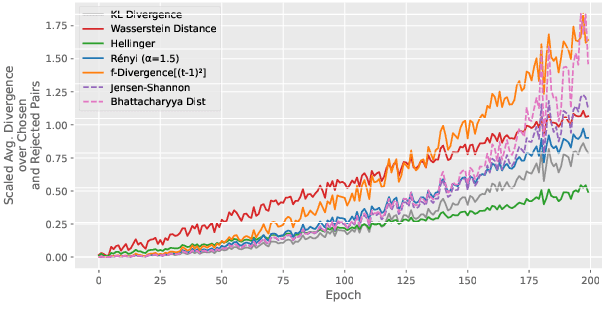
The rapid rise of large language models (LLMs) has unlocked many applications but also underscores the challenge of aligning them with diverse values and preferences. Direct Preference Optimization (DPO) is central to alignment but constrained by fixed divergences and limited feature transformations. We propose DPO-Kernels, which integrates kernel methods to address these issues through four key contributions: (i) Kernelized Representations with polynomial, RBF, Mahalanobis, and spectral kernels for richer transformations, plus a hybrid loss combining embedding-based and probability-based objectives; (ii) Divergence Alternatives (Jensen-Shannon, Hellinger, Renyi, Bhattacharyya, Wasserstein, and f-divergences) for greater stability; (iii) Data-Driven Selection metrics that automatically choose the best kernel-divergence pair; and (iv) a Hierarchical Mixture of Kernels for both local precision and global modeling. Evaluations on 12 datasets demonstrate state-of-the-art performance in factuality, safety, reasoning, and instruction following. Grounded in Heavy-Tailed Self-Regularization, DPO-Kernels maintains robust generalization for LLMs, offering a comprehensive resource for further alignment research.

Iterative NLP Query Refinement for Enhancing Domain-Specific Information Retrieval: A Case Study in Career Services

Retrieving semantically relevant documents in niche domains poses significant challenges for traditional TF-IDF-based systems, often resulting in low similarity scores and suboptimal retrieval performance. This paper addresses these challenges by introducing an iterative and semi-automated query refinement methodology tailored to Humber College's career services webpages. Initially, generic queries related to interview preparation yield low top-document similarities (approximately 0.2--0.3). To enhance retrieval effectiveness, we implement a two-fold approach: first, domain-aware query refinement by incorporating specialized terms such as resources-online-learning, student-online-services, and career-advising; second, the integration of structured educational descriptors like "online resume and interview improvement tools." Additionally, we automate the extraction of domain-specific keywords from top-ranked documents to suggest relevant terms for query expansion. Through experiments conducted on five baseline queries, our semi-automated iterative refinement process elevates the average top similarity score from approximately 0.18 to 0.42, marking a substantial improvement in retrieval performance. The implementation details, including reproducible code and experimental setups, are made available in our GitHub repositories \url{https://github.com/Elipei88/HumberChatbotBackend} and \url{https://github.com/Nisarg851/HumberChatbot}. We also discuss the limitations of our approach and propose future directions, including the integration of advanced neural retrieval models.

Pose Estimation and Tracking for ASIST

Aircraft Ship Integrated Secure and Traverse (ASIST) is a system designed to arrest helicopters safely and efficiently on ships. Originally, a precision Helicopter Position Sensing Equipment (HPSE) tracked and monitored the position of the helicopter relative to the Rapid Securing Device (RSD). However, using the HPSE component was determined to be infeasible in the transition of the ASIST system due to the hardware installation requirements. As a result, sailors track the position of the helicopters with their eyes with no sensor or artificially intelligent decision aid. Manually tracking the helicopter takes additional time and makes recoveries more difficult, especially at high sea states. Performing recoveries without the decision aid leads to higher uncertainty and cognitive load. PETA (Pose Estimation and Tracking for ASIST) is a research effort to create a helicopter tracking system prototype without hardware installation requirements for ASIST system operators. Its overall goal is to improve situational awareness and reduce operator uncertainty with respect to the aircrafts position relative to the RSD, and consequently increase the allowable landing area. The authors produced a prototype system capable of tracking helicopters with respect to the RSD. The software included a helicopter pose estimation component, camera pose estimation component, and a user interface component. PETA demonstrated the potential for state-of-the-art computer vision algorithms Faster R-CNN and HRNet (High-Resolution Network) to be used to estimate the pose of helicopters in real-time, returning ASIST to its originally intended capability. PETA also demonstrated that traditional methods of encoder-decoders could be used to estimate the orientation of the helicopter and could be used to confirm the output from HRNet.

Computer Vision for Carriers: PATRIOT

Deck tracking performed on carriers currently involves a team of sailors manually identifying aircraft and updating a digital user interface called the Ouija Board. Improvements to the deck tracking process would result in increased Sortie Generation Rates, and therefore applying automation is seen as a critical method to improve deck tracking. However, the requirements on a carrier ship do not allow for the installation of hardware-based location sensing technologies like Global Positioning System (GPS) sensors. PATRIOT (Panoramic Asset Tracking of Real-Time Information for the Ouija Tabletop) is a research effort and proposed solution to performing deck tracking with passive sensing and without the need for GPS sensors. PATRIOT is a prototype system which takes existing camera feeds, calculates aircraft poses, and updates a virtual Ouija board interface with the current status of the assets. PATRIOT would allow for faster, more accurate, and less laborious asset tracking for aircraft, people, and support equipment. PATRIOT is anticipated to benefit the warfighter by reducing cognitive workload, reducing manning requirements, collecting data to improve logistics, and enabling an automation gateway for future efforts to improve efficiency and safety. The authors have developed and tested algorithms to perform pose estimations of assets in real-time including OpenPifPaf, High-Resolution Network (HRNet), HigherHRNet (HHRNet), Faster R-CNN, and in-house developed encoder-decoder network. The software was tested with synthetic and real-world data and was able to accurately extract the pose of assets. Fusion, tracking, and real-world generality are planned to be improved to ensure a successful transition to the fleet.

Scalable Uni-directional Pareto Optimality for Multi-Task Learning with Constraints

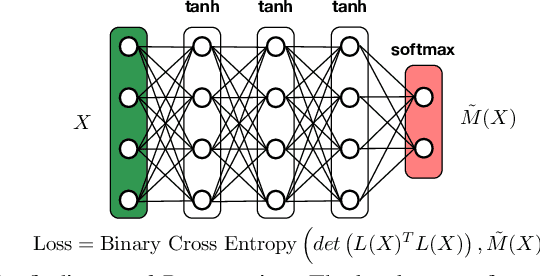
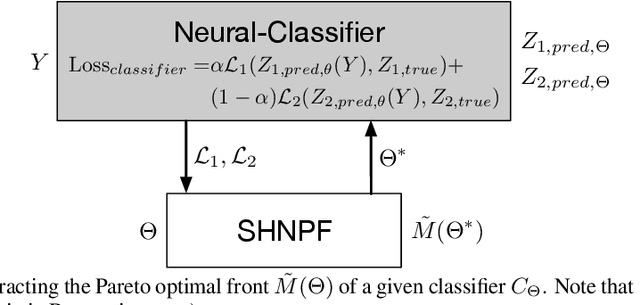
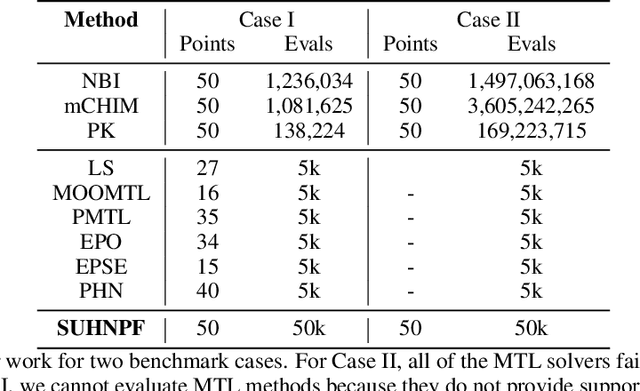
We propose a scalable Pareto solver for Multi-Objective Optimization (MOO) problems, including support for optimization under constraints. An important application of this solver is to estimate high-dimensional neural models for MOO classification tasks. We demonstrate significant runtime and space improvement using our solver \vs prior methods, verify that solutions found are truly Pareto optimal on a benchmark set of known non-convex MOO problems from {\em operations research}, and provide a practical evaluation against prior methods for Multi-Task Learning (MTL).

Tail-Net: Extracting Lowest Singular Triplets for Big Data Applications

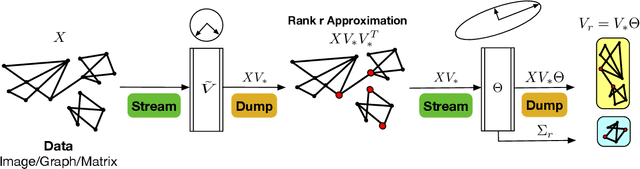
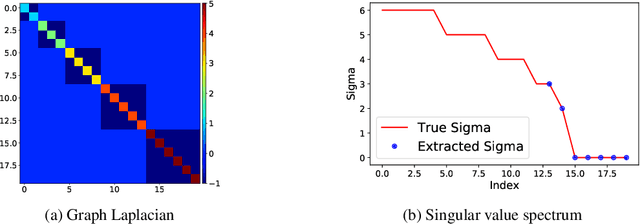
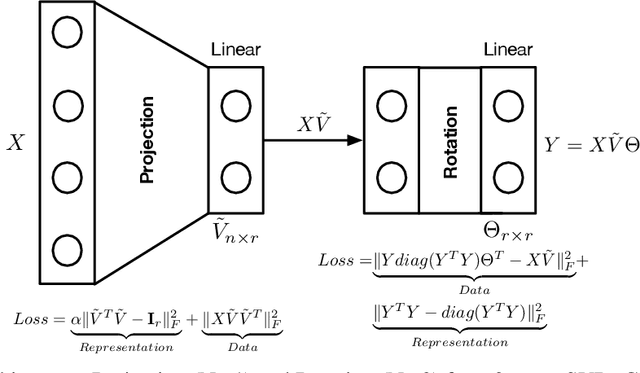
SVD serves as an exploratory tool in identifying the dominant features in the form of top rank-r singular factors corresponding to the largest singular values. For Big Data applications it is well known that Singular Value Decomposition (SVD) is restrictive due to main memory requirements. However, a number of applications such as community detection, clustering, or bottleneck identification in large scale graph data-sets rely upon identifying the lowest singular values and the singular corresponding vectors. For example, the lowest singular values of a graph Laplacian reveal the number of isolated clusters (zero singular values) or bottlenecks (lowest non-zero singular values) for undirected, acyclic graphs. A naive approach here would be to perform a full SVD however, this quickly becomes infeasible for practical big data applications due to the enormous memory requirements. Furthermore, for such applications only a few lowest singular factors are desired making a full decomposition computationally exorbitant. In this work, we trivially extend the previously proposed Range-Net to \textbf{Tail-Net} for a memory and compute efficient extraction of lowest singular factors of a given big dataset and a specified rank-r. We present a number of numerical experiments on both synthetic and practical data-sets for verification and bench-marking using conventional SVD as the baseline.