Fairly Accurate: Optimizing Accuracy Parity in Fair Target-Group Detection

In algorithmic toxicity detection pipelines, it is important to identify which demographic group(s) are the subject of a post, a task commonly known as \textit{target (group) detection}. While accurate detection is clearly important, we further advocate a fairness objective: to provide equal protection to all groups who may be targeted. To this end, we adopt \textit{Accuracy Parity} (AP) -- balanced detection accuracy across groups -- as our fairness objective. However, in order to align model training with our AP fairness objective, we require an equivalent loss function. Moreover, for gradient-based models such as neural networks, this loss function needs to be differentiable. Because no such loss function exists today for AP, we propose \emph{Group Accuracy Parity} (GAP): the first differentiable loss function having a one-on-one mapping to AP. We empirically show that GAP addresses disparate impact on groups for target detection. Furthermore, because a single post often targets multiple groups in practice, we also provide a mathematical extension of GAP to larger multi-group settings, something typically requiring heuristics in prior work. Our findings show that by optimizing AP, GAP better mitigates bias in comparison with other commonly employed loss functions.

Same Same, But Different: Conditional Multi-Task Learning for Demographic-Specific Toxicity Detection

Algorithmic bias often arises as a result of differential subgroup validity, in which predictive relationships vary across groups. For example, in toxic language detection, comments targeting different demographic groups can vary markedly across groups. In such settings, trained models can be dominated by the relationships that best fit the majority group, leading to disparate performance. We propose framing toxicity detection as multi-task learning (MTL), allowing a model to specialize on the relationships that are relevant to each demographic group while also leveraging shared properties across groups. With toxicity detection, each task corresponds to identifying toxicity against a particular demographic group. However, traditional MTL requires labels for all tasks to be present for every data point. To address this, we propose Conditional MTL (CondMTL), wherein only training examples relevant to the given demographic group are considered by the loss function. This lets us learn group specific representations in each branch which are not cross contaminated by irrelevant labels. Results on synthetic and real data show that using CondMTL improves predictive recall over various baselines in general and for the minority demographic group in particular, while having similar overall accuracy.

Fairly Accurate: Learning Optimal Accuracy vs. Fairness Tradeoffs for Hate Speech Detection

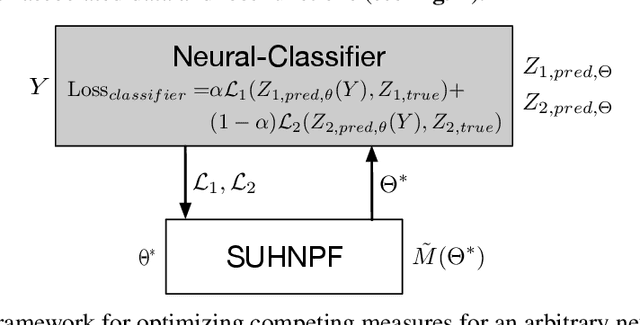
Recent work has emphasized the importance of balancing competing objectives in model training (e.g., accuracy vs. fairness, or competing measures of fairness). Such trade-offs reflect a broader class of multi-objective optimization (MOO) problems in which optimization methods seek Pareto optimal trade-offs between competing goals. In this work, we first introduce a differentiable measure that enables direct optimization of group fairness (specifically, balancing accuracy across groups) in model training. Next, we demonstrate two model-agnostic MOO frameworks for learning Pareto optimal parameterizations over different groups of neural classification models. We evaluate our methods on the specific task of hate speech detection, in which prior work has shown lack of group fairness across speakers of different English dialects. Empirical results across convolutional, sequential, and transformer-based neural architectures show superior empirical accuracy vs. fairness trade-offs over prior work. More significantly, our measure enables the Pareto machinery to ensure that each architecture achieves the best possible trade-off between fairness and accuracy w.r.t. the dataset, given user-prescribed error tolerance bounds.

Scalable Uni-directional Pareto Optimality for Multi-Task Learning with Constraints

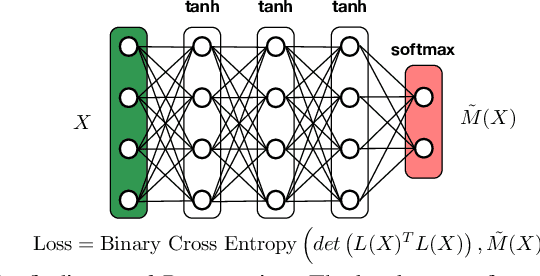
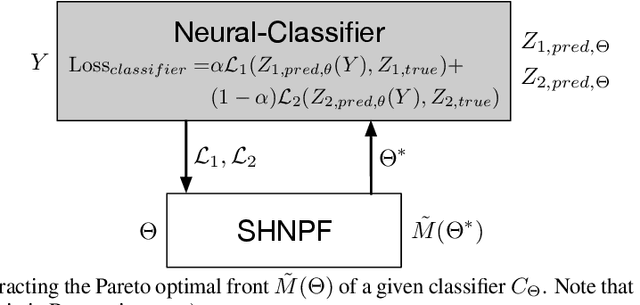
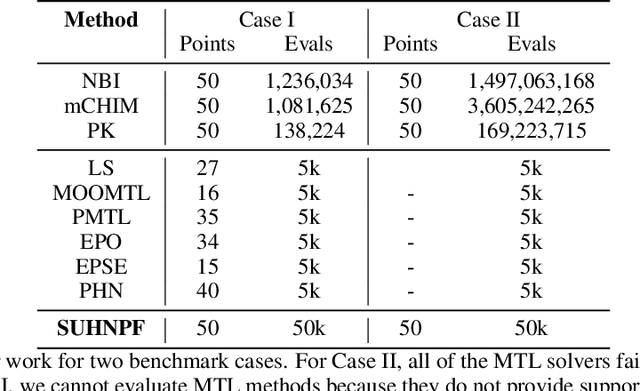
We propose a scalable Pareto solver for Multi-Objective Optimization (MOO) problems, including support for optimization under constraints. An important application of this solver is to estimate high-dimensional neural models for MOO classification tasks. We demonstrate significant runtime and space improvement using our solver \vs prior methods, verify that solutions found are truly Pareto optimal on a benchmark set of known non-convex MOO problems from {\em operations research}, and provide a practical evaluation against prior methods for Multi-Task Learning (MTL).

Tail-Net: Extracting Lowest Singular Triplets for Big Data Applications

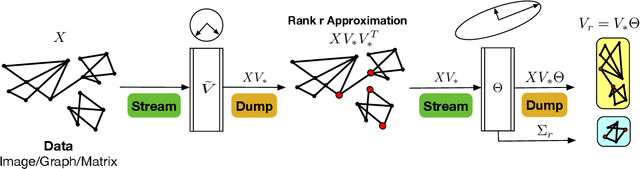
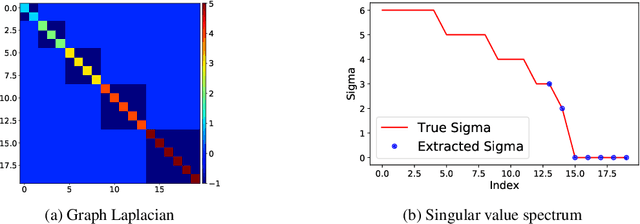
SVD serves as an exploratory tool in identifying the dominant features in the form of top rank-r singular factors corresponding to the largest singular values. For Big Data applications it is well known that Singular Value Decomposition (SVD) is restrictive due to main memory requirements. However, a number of applications such as community detection, clustering, or bottleneck identification in large scale graph data-sets rely upon identifying the lowest singular values and the singular corresponding vectors. For example, the lowest singular values of a graph Laplacian reveal the number of isolated clusters (zero singular values) or bottlenecks (lowest non-zero singular values) for undirected, acyclic graphs. A naive approach here would be to perform a full SVD however, this quickly becomes infeasible for practical big data applications due to the enormous memory requirements. Furthermore, for such applications only a few lowest singular factors are desired making a full decomposition computationally exorbitant. In this work, we trivially extend the previously proposed Range-Net to \textbf{Tail-Net} for a memory and compute efficient extraction of lowest singular factors of a given big dataset and a specified rank-r. We present a number of numerical experiments on both synthetic and practical data-sets for verification and bench-marking using conventional SVD as the baseline.

SCA-Net: A Self-Correcting Two-Layer Autoencoder for Hyper-spectral Unmixing

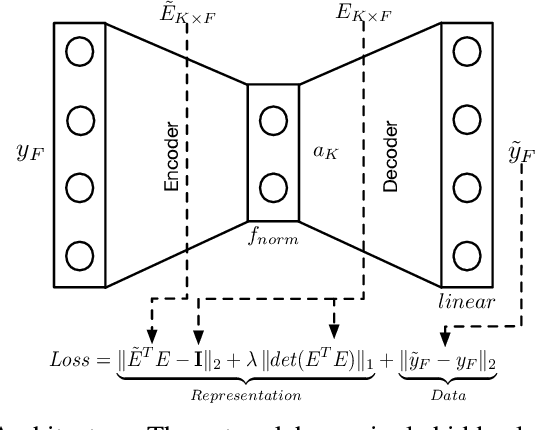
Linear Mixture Model for hyperspectral datasets involves separating a mixed pixel as a linear combination of its constituent endmembers and corresponding fractional abundances. Both optimization and neural methods have attempted to tackle this problem, with the current state of the art results achieved by neural models on benchmark datasets. However, our review of these neural models show that these networks are severely over-parameterized and consequently the invariant endmember spectra extracted as decoder weights has a high variance over multiple runs. All of these approaches require substantial post-processing to satisfy LMM constraints. Furthermore, they also require an exact specification of the number of endmembers and specialized initialization of weights from other algorithms like VCA. Our work shows for the first time that a two-layer autoencoder (SCA-Net), with $2FK$ parameters ($F$ features, $K$ endmembers), achieves error metrics that are scales apart ($10^{-5})$ from previously reported values $(10^{-2})$. SCA-Net converges to this low error solution starting from a random initialization of weights. We also show that SCA-Net, based upon a bi-orthogonal representation, performs a self-correction when the the number of endmembers are over-specified. We show that our network formulation extracts a low-rank representation that is bounded below by a tail-energy and can be computationally verified. Our numerical experiments on Samson, Jasper, and Urban datasets demonstrate that SCA-Net outperforms previously reported error metrics for all the cases while being robust to noise and outliers.

A Hybrid 2-stage Neural Optimization for Pareto Front Extraction

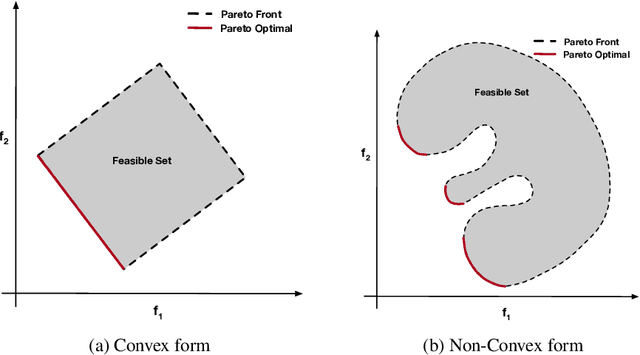
Classification, recommendation, and ranking problems often involve competing goals with additional constraints (e.g., to satisfy fairness or diversity criteria). Such optimization problems are quite challenging, often involving non-convex functions along with considerations of user preferences in balancing trade-offs. Pareto solutions represent optimal frontiers for jointly optimizing multiple competing objectives. A major obstacle for frequently used linear-scalarization strategies is that the resulting optimization problem might not always converge to a global optimum. Furthermore, such methods only return one solution point per run. A Pareto solution set is a subset of all such global optima over multiple runs for different trade-off choices. Therefore, a Pareto front can only be guaranteed with multiple runs of the linear-scalarization problem, where all runs converge to their respective global optima. Consequently, extracting a Pareto front for practical problems is computationally intractable with substantial computational overheads, limited scalability, and reduced accuracy. We propose a robust, low cost, two-stage, hybrid neural Pareto optimization approach that is accurate and scales (compute space and time) with data dimensions, as well as number of functions and constraints. The first stage (neural network) efficiently extracts a weak Pareto front, using Fritz-John conditions as the discriminator, with no assumptions of convexity on the objectives or constraints. The second stage (efficient Pareto filter) extracts the strong Pareto optimal subset given the weak front from stage 1. Fritz-John conditions provide us with theoretical bounds on approximation error between the true and network extracted weak Pareto front. Numerical experiments demonstrates the accuracy and efficiency on a canonical set of benchmark problems and a fairness optimization task from prior works.

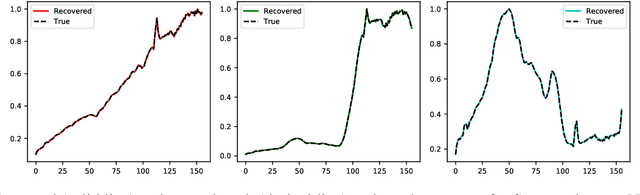
Streaming Singular Value Decomposition for Big Data Applications

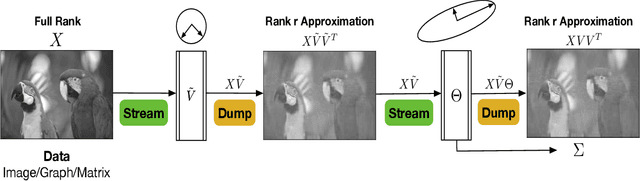
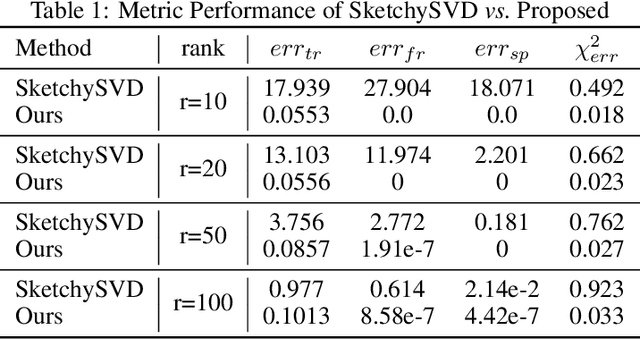
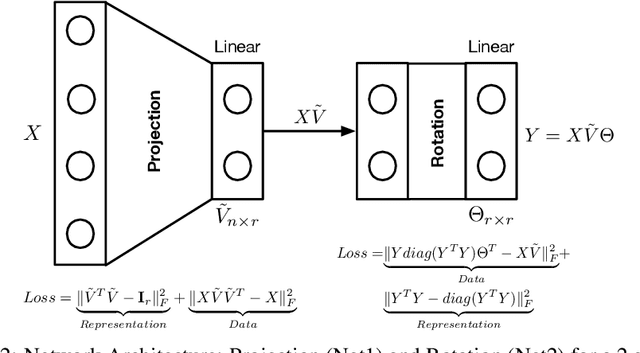
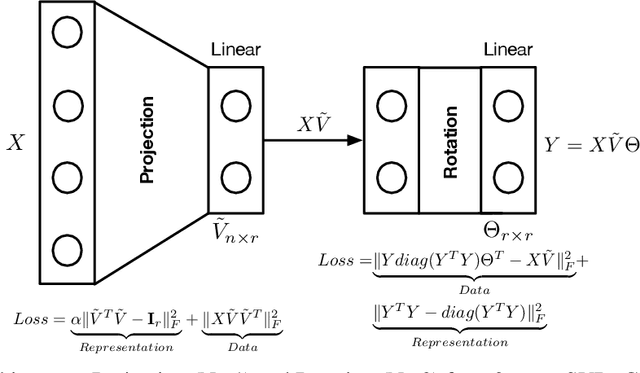
Singular Value Decomposition (SVD) plays a pivotal role in exploratory data analysis. However, in a Big Data setting computing the dominant singular vectors is often restrictive due to the main memory requirements imposed by the dataset. Recently introduced randomized projection schemes attempt to mitigate this memory load by constructing approximate projections of the true dataset in a streaming setting. However, these projection methods come at the cost of approximation errors in both top singular values and vectors. Furthermore, in order to bound the approximation error, an over-sampled projection is required, often much larger in dimension than the desired rank. This latter consideration can still be memory intensive when the data dimension is large or extraneous when the desired rank approximation is close to the full rank. We present a two stage neural optimization approach as an alternative to conventional and randomized SVD techniques, where the memory requirement depends explicitly on the feature dimension and desired rank, independent of the sample size. The proposed scheme reads data samples in a streaming setting with the network minimization problem converging to a low rank approximation with high precision. Our architecture is fully interpretable where all the network outputs and weights have a specific meaning. We evaluate our results on various performance metrics against state of the art streaming methods. We also present numerical experiments for Singular and Eigen value decomposition on real data at various scales to show the memory efficiency of our proposed approach.

Extracting Optimal Solution Manifolds using Constrained Neural Optimization

Constrained Optimization solution algorithms are restricted to point based solutions. In practice, single or multiple objectives must be satisfied, wherein both the objective function and constraints can be non-convex resulting in multiple optimal solutions. Real world scenarios include intersecting surfaces as Implicit Functions, Hyperspectral Unmixing and Pareto Optimal fronts. Local or global convexification is a common workaround when faced with non-convex forms. However, such an approach is often restricted to a strict class of functions, deviation from which results in sub-optimal solution to the original problem. We present neural solutions for extracting optimal sets as approximate manifolds, where unmodified, non-convex objectives and constraints are defined as modeler guided, domain-informed $L_2$ loss function. This promotes interpretability since modelers can confirm the results against known analytical forms in their specific domains. We present synthetic and realistic cases to validate our approach and compare against known solvers for bench-marking in terms of accuracy and computational efficiency.

Prevention is Better than Cure: Handling Basis Collapse and Transparency in Dense Networks

Dense nets are an integral part of any classification and regression problem. Recently, these networks have found a new application as solvers for known representations in various domains. However, one crucial issue with dense nets is it's feature interpretation and lack of reproducibility over multiple training runs. In this work, we identify a basis collapse issue as a primary cause and propose a modified loss function that circumvents this problem. We also provide a few general guidelines relating the choice of activations to loss surface roughness and appropriate scaling for designing low-weight dense nets. We demonstrate through carefully chosen numerical experiments that the basis collapse issue leads to the design of massively redundant networks. Our approach results in substantially concise nets, having $100 \times$ fewer parameters, while achieving a much lower $(10\times)$ MSE loss at scale than reported in prior works. Further, we show that the width of a dense net is acutely dependent on the feature complexity. This is in contrast to the dimension dependent width choice reported in prior theoretical works. To the best of our knowledge, this is the first time these issues and contradictions have been reported and experimentally verified. With our design guidelines we render transparency in terms of a low-weight network design. We share our codes for full reproducibility available at https://github.com/smjtgupta/Dense_Net_Regress.