SCA-Net: A Self-Correcting Two-Layer Autoencoder for Hyper-spectral Unmixing
Paper and Code
Feb 22, 2021
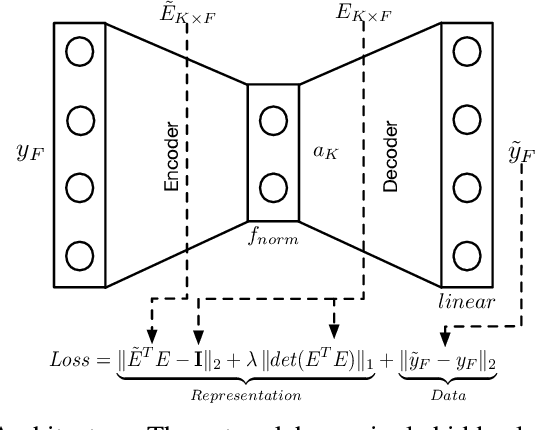

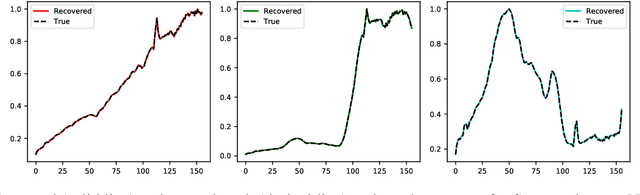
Linear Mixture Model for hyperspectral datasets involves separating a mixed pixel as a linear combination of its constituent endmembers and corresponding fractional abundances. Both optimization and neural methods have attempted to tackle this problem, with the current state of the art results achieved by neural models on benchmark datasets. However, our review of these neural models show that these networks are severely over-parameterized and consequently the invariant endmember spectra extracted as decoder weights has a high variance over multiple runs. All of these approaches require substantial post-processing to satisfy LMM constraints. Furthermore, they also require an exact specification of the number of endmembers and specialized initialization of weights from other algorithms like VCA. Our work shows for the first time that a two-layer autoencoder (SCA-Net), with $2FK$ parameters ($F$ features, $K$ endmembers), achieves error metrics that are scales apart ($10^{-5})$ from previously reported values $(10^{-2})$. SCA-Net converges to this low error solution starting from a random initialization of weights. We also show that SCA-Net, based upon a bi-orthogonal representation, performs a self-correction when the the number of endmembers are over-specified. We show that our network formulation extracts a low-rank representation that is bounded below by a tail-energy and can be computationally verified. Our numerical experiments on Samson, Jasper, and Urban datasets demonstrate that SCA-Net outperforms previously reported error metrics for all the cases while being robust to noise and outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge