Tail-Net: Extracting Lowest Singular Triplets for Big Data Applications
Paper and Code
Apr 28, 2021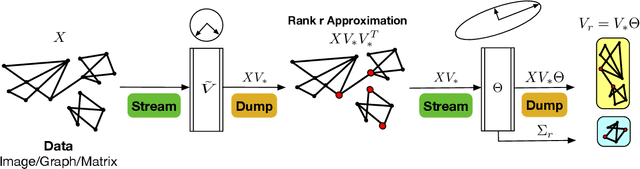
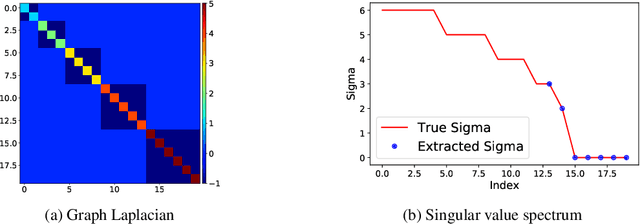
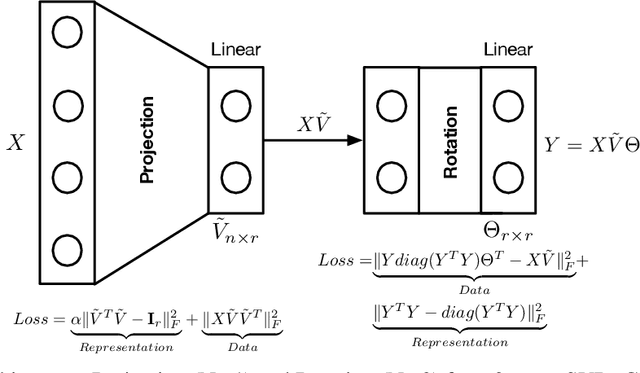

SVD serves as an exploratory tool in identifying the dominant features in the form of top rank-r singular factors corresponding to the largest singular values. For Big Data applications it is well known that Singular Value Decomposition (SVD) is restrictive due to main memory requirements. However, a number of applications such as community detection, clustering, or bottleneck identification in large scale graph data-sets rely upon identifying the lowest singular values and the singular corresponding vectors. For example, the lowest singular values of a graph Laplacian reveal the number of isolated clusters (zero singular values) or bottlenecks (lowest non-zero singular values) for undirected, acyclic graphs. A naive approach here would be to perform a full SVD however, this quickly becomes infeasible for practical big data applications due to the enormous memory requirements. Furthermore, for such applications only a few lowest singular factors are desired making a full decomposition computationally exorbitant. In this work, we trivially extend the previously proposed Range-Net to \textbf{Tail-Net} for a memory and compute efficient extraction of lowest singular factors of a given big dataset and a specified rank-r. We present a number of numerical experiments on both synthetic and practical data-sets for verification and bench-marking using conventional SVD as the baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge