Streaming Singular Value Decomposition for Big Data Applications
Paper and Code
Oct 27, 2020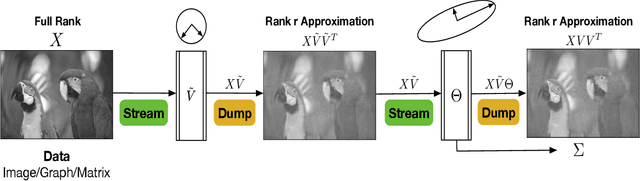
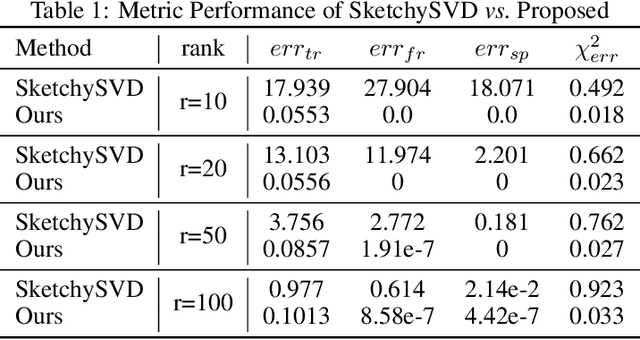
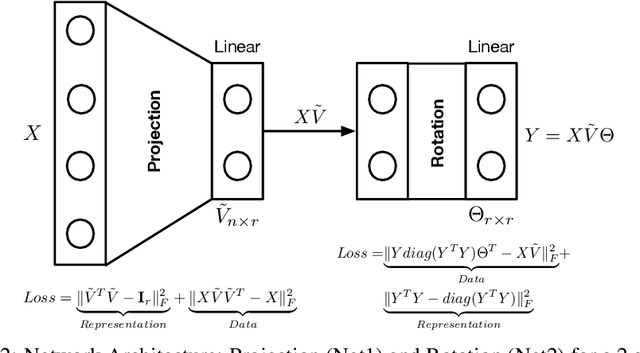
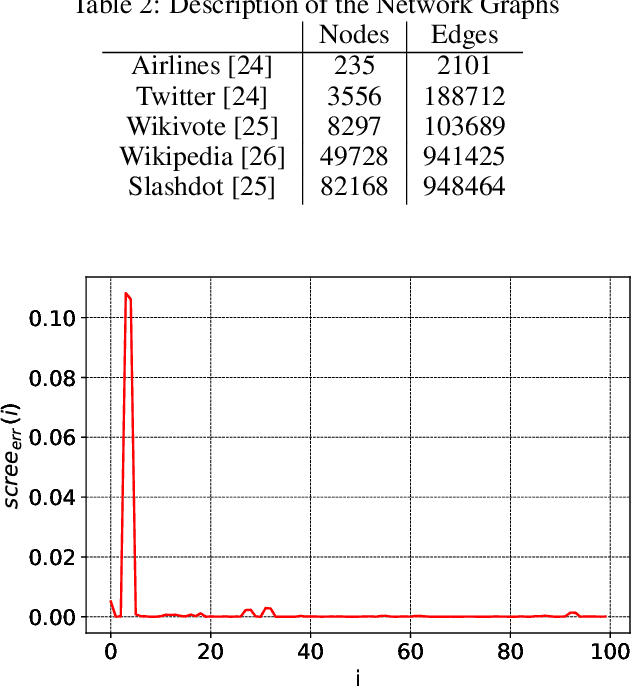
Singular Value Decomposition (SVD) plays a pivotal role in exploratory data analysis. However, in a Big Data setting computing the dominant singular vectors is often restrictive due to the main memory requirements imposed by the dataset. Recently introduced randomized projection schemes attempt to mitigate this memory load by constructing approximate projections of the true dataset in a streaming setting. However, these projection methods come at the cost of approximation errors in both top singular values and vectors. Furthermore, in order to bound the approximation error, an over-sampled projection is required, often much larger in dimension than the desired rank. This latter consideration can still be memory intensive when the data dimension is large or extraneous when the desired rank approximation is close to the full rank. We present a two stage neural optimization approach as an alternative to conventional and randomized SVD techniques, where the memory requirement depends explicitly on the feature dimension and desired rank, independent of the sample size. The proposed scheme reads data samples in a streaming setting with the network minimization problem converging to a low rank approximation with high precision. Our architecture is fully interpretable where all the network outputs and weights have a specific meaning. We evaluate our results on various performance metrics against state of the art streaming methods. We also present numerical experiments for Singular and Eigen value decomposition on real data at various scales to show the memory efficiency of our proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge