A Hybrid 2-stage Neural Optimization for Pareto Front Extraction
Paper and Code
Feb 13, 2021
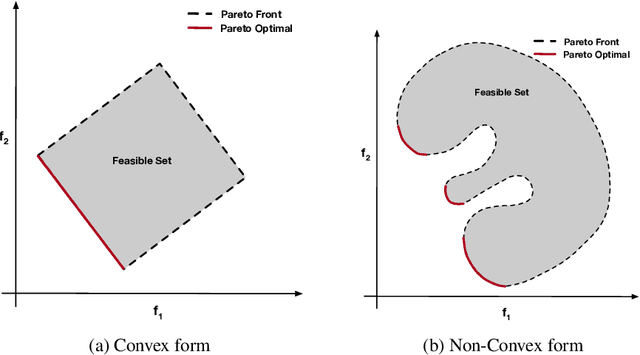


Classification, recommendation, and ranking problems often involve competing goals with additional constraints (e.g., to satisfy fairness or diversity criteria). Such optimization problems are quite challenging, often involving non-convex functions along with considerations of user preferences in balancing trade-offs. Pareto solutions represent optimal frontiers for jointly optimizing multiple competing objectives. A major obstacle for frequently used linear-scalarization strategies is that the resulting optimization problem might not always converge to a global optimum. Furthermore, such methods only return one solution point per run. A Pareto solution set is a subset of all such global optima over multiple runs for different trade-off choices. Therefore, a Pareto front can only be guaranteed with multiple runs of the linear-scalarization problem, where all runs converge to their respective global optima. Consequently, extracting a Pareto front for practical problems is computationally intractable with substantial computational overheads, limited scalability, and reduced accuracy. We propose a robust, low cost, two-stage, hybrid neural Pareto optimization approach that is accurate and scales (compute space and time) with data dimensions, as well as number of functions and constraints. The first stage (neural network) efficiently extracts a weak Pareto front, using Fritz-John conditions as the discriminator, with no assumptions of convexity on the objectives or constraints. The second stage (efficient Pareto filter) extracts the strong Pareto optimal subset given the weak front from stage 1. Fritz-John conditions provide us with theoretical bounds on approximation error between the true and network extracted weak Pareto front. Numerical experiments demonstrates the accuracy and efficiency on a canonical set of benchmark problems and a fairness optimization task from prior works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge