Tan Bui-Thanh
Department of Aerospace Engineering and Engineering Mechanics, the University of Texas at Austin, Texas, The Oden Institute for Computational Engineering and Sciences, the University of Texas at Austin, Texas
Topological derivative approach for deep neural network architecture adaptation
Feb 08, 2025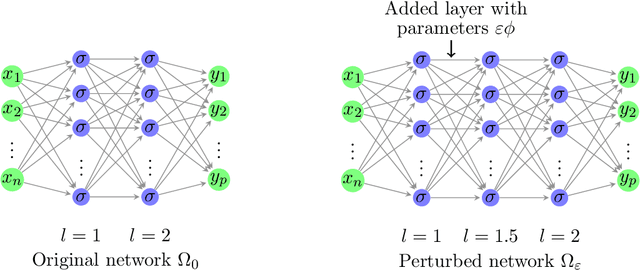

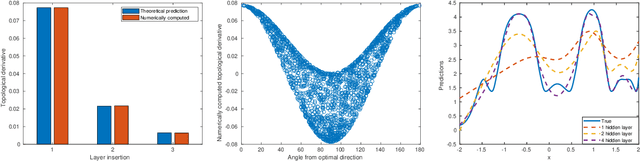
Abstract:This work presents a novel algorithm for progressively adapting neural network architecture along the depth. In particular, we attempt to address the following questions in a mathematically principled way: i) Where to add a new capacity (layer) during the training process? ii) How to initialize the new capacity? At the heart of our approach are two key ingredients: i) the introduction of a ``shape functional" to be minimized, which depends on neural network topology, and ii) the introduction of a topological derivative of the shape functional with respect to the neural network topology. Using an optimal control viewpoint, we show that the network topological derivative exists under certain conditions, and its closed-form expression is derived. In particular, we explore, for the first time, the connection between the topological derivative from a topology optimization framework with the Hamiltonian from optimal control theory. Further, we show that the optimality condition for the shape functional leads to an eigenvalue problem for deep neural architecture adaptation. Our approach thus determines the most sensitive location along the depth where a new layer needs to be inserted during the training phase and the associated parametric initialization for the newly added layer. We also demonstrate that our layer insertion strategy can be derived from an optimal transport viewpoint as a solution to maximizing a topological derivative in $p$-Wasserstein space, where $p>= 1$. Numerical investigations with fully connected network, convolutional neural network, and vision transformer on various regression and classification problems demonstrate that our proposed approach can outperform an ad-hoc baseline network and other architecture adaptation strategies. Further, we also demonstrate other applications of topological derivative in fields such as transfer learning.
A Constant Velocity Latent Dynamics Approach for Accelerating Simulation of Stiff Nonlinear Systems
Jan 14, 2025Abstract:Solving stiff ordinary differential equations (StODEs) requires sophisticated numerical solvers, which are often computationally expensive. In particular, StODE's often cannot be solved with traditional explicit time integration schemes and one must resort to costly implicit methods to compute solutions. On the other hand, state-of-the-art machine learning (ML) based methods such as Neural ODE (NODE) poorly handle the timescale separation of various elements of the solutions to StODEs and require expensive implicit solvers for integration at inference time. In this work, we embark on a different path which involves learning a latent dynamics for StODEs, in which one completely avoids numerical integration. To that end, we consider a constant velocity latent dynamical system whose solution is a sequence of straight lines. Given the initial condition and parameters of the ODE, the encoder networks learn the slope (i.e the constant velocity) and the initial condition for the latent dynamics. In other words, the solution of the original dynamics is encoded into a sequence of straight lines which can be decoded back to retrieve the actual solution as and when required. Another key idea in our approach is a nonlinear transformation of time, which allows for the "stretching/squeezing" of time in the latent space, thereby allowing for varying levels of attention to different temporal regions in the solution. Additionally, we provide a simple universal-approximation-type proof showing that our approach can approximate the solution of stiff nonlinear system on a compact set to any degree of accuracy, {\epsilon}. We show that the dimension of the latent dynamical system in our approach is independent of {\epsilon}. Numerical investigation on prototype StODEs suggest that our method outperforms state-of-the art machine learning approaches for handling StODEs.
TAE: A Model-Constrained Tikhonov Autoencoder Approach for Forward and Inverse Problems
Dec 09, 2024



Abstract:Efficient real-time solvers for forward and inverse problems are essential in engineering and science applications. Machine learning surrogate models have emerged as promising alternatives to traditional methods, offering substantially reduced computational time. Nevertheless, these models typically demand extensive training datasets to achieve robust generalization across diverse scenarios. While physics-based approaches can partially mitigate this data dependency and ensure physics-interpretable solutions, addressing scarce data regimes remains a challenge. Both purely data-driven and physics-based machine learning approaches demonstrate severe overfitting issues when trained with insufficient data. We propose a novel Tikhonov autoencoder model-constrained framework, called TAE, capable of learning both forward and inverse surrogate models using a single arbitrary observation sample. We develop comprehensive theoretical foundations including forward and inverse inference error bounds for the proposed approach for linear cases. For comparative analysis, we derive equivalent formulations for pure data-driven and model-constrained approach counterparts. At the heart of our approach is a data randomization strategy, which functions as a generative mechanism for exploring the training data space, enabling effective training of both forward and inverse surrogate models from a single observation, while regularizing the learning process. We validate our approach through extensive numerical experiments on two challenging inverse problems: 2D heat conductivity inversion and initial condition reconstruction for time-dependent 2D Navier-Stokes equations. Results demonstrate that TAE achieves accuracy comparable to traditional Tikhonov solvers and numerical forward solvers for both inverse and forward problems, respectively, while delivering orders of magnitude computational speedups.
A model-constrained Discontinuous Galerkin Network (DGNet) for Compressible Euler Equations with Out-of-Distribution Generalization
Sep 27, 2024



Abstract:Real-time accurate solutions of large-scale complex dynamical systems are critically needed for control, optimization, uncertainty quantification, and decision-making in practical engineering and science applications, particularly in digital twin contexts. In this work, we develop a model-constrained discontinuous Galerkin Network (DGNet) approach, an extension to our previous work [Model-constrained Tagent Slope Learning Approach for Dynamical Systems], for compressible Euler equations with out-of-distribution generalization. The core of DGNet is the synergy of several key strategies: (i) leveraging time integration schemes to capture temporal correlation and taking advantage of neural network speed for computation time reduction; (ii) employing a model-constrained approach to ensure the learned tangent slope satisfies governing equations; (iii) utilizing a GNN-inspired architecture where edges represent Riemann solver surrogate models and nodes represent volume integration correction surrogate models, enabling capturing discontinuity capacity, aliasing error reduction, and mesh discretization generalizability; (iv) implementing the input normalization technique that allows surrogate models to generalize across different initial conditions, boundary conditions, and solution orders; and (v) incorporating a data randomization technique that not only implicitly promotes agreement between surrogate models and true numerical models up to second-order derivatives, ensuring long-term stability and prediction capacity, but also serves as a data generation engine during training, leading to enhanced generalization on unseen data. To validate the effectiveness, stability, and generalizability of our novel DGNet approach, we present comprehensive numerical results for 1D and 2D compressible Euler equation problems.
An autoencoder compression approach for accelerating large-scale inverse problems
Apr 10, 2023Abstract:PDE-constrained inverse problems are some of the most challenging and computationally demanding problems in computational science today. Fine meshes that are required to accurately compute the PDE solution introduce an enormous number of parameters and require large scale computing resources such as more processors and more memory to solve such systems in a reasonable time. For inverse problems constrained by time dependent PDEs, the adjoint method that is often employed to efficiently compute gradients and higher order derivatives requires solving a time-reversed, so-called adjoint PDE that depends on the forward PDE solution at each timestep. This necessitates the storage of a high dimensional forward solution vector at every timestep. Such a procedure quickly exhausts the available memory resources. Several approaches that trade additional computation for reduced memory footprint have been proposed to mitigate the memory bottleneck, including checkpointing and compression strategies. In this work, we propose a close-to-ideal scalable compression approach using autoencoders to eliminate the need for checkpointing and substantial memory storage, thereby reducing both the time-to-solution and memory requirements. We compare our approach with checkpointing and an off-the-shelf compression approach on an earth-scale ill-posed seismic inverse problem. The results verify the expected close-to-ideal speedup for both the gradient and Hessian-vector product using the proposed autoencoder compression approach. To highlight the usefulness of the proposed approach, we combine the autoencoder compression with the data-informed active subspace (DIAS) prior to show how the DIAS method can be affordably extended to large scale problems without the need of checkpointing and large memory.
Layerwise Sparsifying Training and Sequential Learning Strategy for Neural Architecture Adaptation
Nov 13, 2022Abstract:This work presents a two-stage framework for progressively developing neural architectures to adapt/ generalize well on a given training data set. In the first stage, a manifold-regularized layerwise sparsifying training approach is adopted where a new layer is added each time and trained independently by freezing parameters in the previous layers. In order to constrain the functions that should be learned by each layer, we employ a sparsity regularization term, manifold regularization term and a physics-informed term. We derive the necessary conditions for trainability of a newly added layer and analyze the role of manifold regularization. In the second stage of the Algorithm, a sequential learning process is adopted where a sequence of small networks is employed to extract information from the residual produced in stage I and thereby making robust and more accurate predictions. Numerical investigations with fully connected network on prototype regression problem, and classification problem demonstrate that the proposed approach can outperform adhoc baseline networks. Further, application to physics-informed neural network problems suggests that the method could be employed for creating interpretable hidden layers in a deep network while outperforming equivalent baseline networks.
A Model-Constrained Tangent Manifold Learning Approach for Dynamical Systems
Aug 09, 2022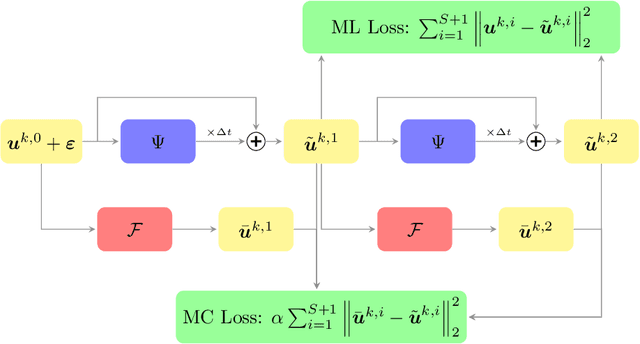
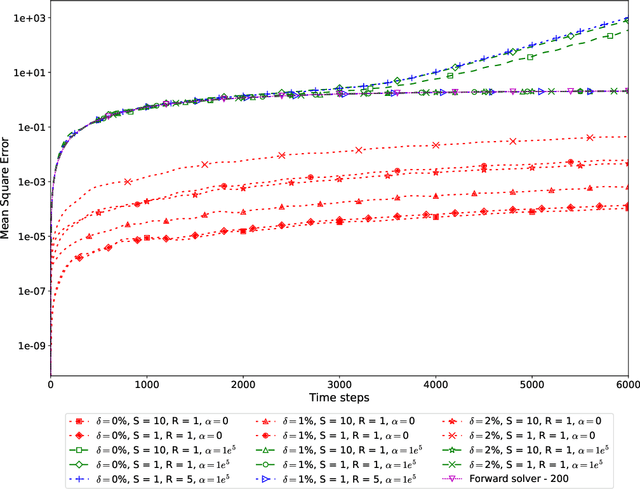
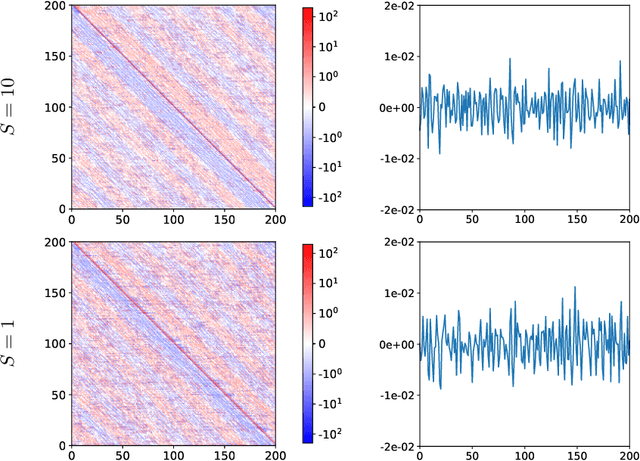
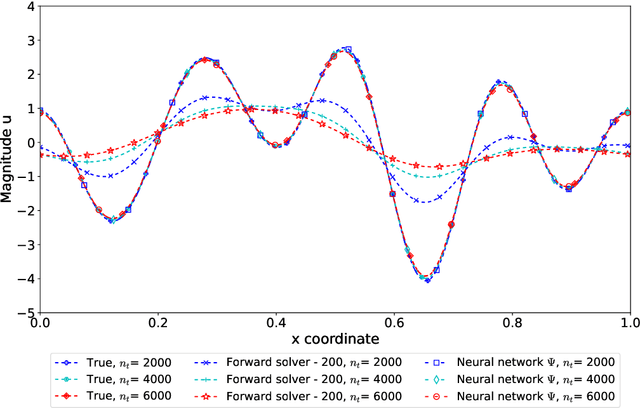
Abstract:Real time accurate solutions of large scale complex dynamical systems are in critical need for control, optimization, uncertainty quantification, and decision-making in practical engineering and science applications. This paper contributes in this direction a model constrained tangent manifold learning (mcTangent) approach. At the heart of mcTangent is the synergy of several desirable strategies: i) a tangent manifold learning to take advantage of the neural network speed and the time accurate nature of the method of lines; ii) a model constrained approach to encode the neural network tangent with the underlying governing equations; iii) sequential learning strategies to promote long time stability and accuracy; and iv) data randomization approach to implicitly enforce the smoothness of the neural network tangent and its likeliness to the truth tangent up second order derivatives in order to further enhance the stability and accuracy of mcTangent solutions. Both semi heuristic and rigorous arguments are provided to analyze and justify the proposed approach. Several numerical results for transport equation, viscous Burgers equation, and Navier Stokes equation are presented to study and demonstrate the capability of the proposed mcTangent learning approach.
A Unified and Constructive Framework for the Universality of Neural Networks
Jan 07, 2022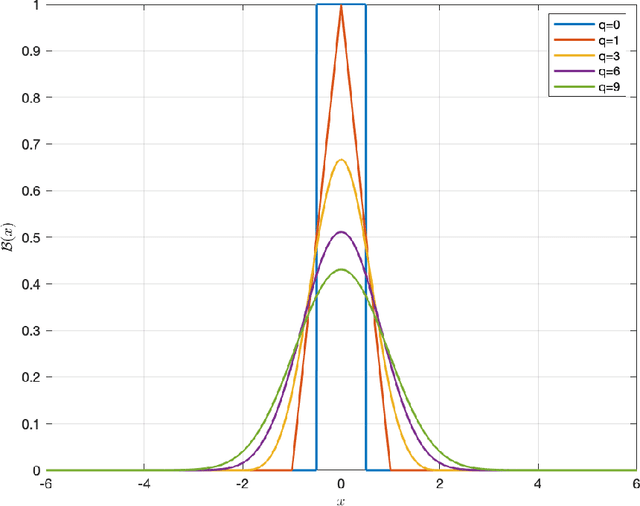

Abstract:One of the reasons why many neural networks are capable of replicating complicated tasks or functions is their universal property. Though the past few decades have seen tremendous advances in theories of neural networks, a single constructive framework for neural network universality remains unavailable. This paper is an effort to provide a unified and constructive framework for the universality of a large class of activations including most of existing ones. At the heart of the framework is the concept of neural network approximate identity (nAI). The main result is: {\em any nAI activation function is universal}. It turns out that most of existing activations are nAI, and thus universal in the space of continuous functions on compacta. The framework has the following main properties. First, it is constructive with elementary means from functional analysis, probability theory, and numerical analysis. Second, it is the first unified attempt that is valid for most of existing activations. Third, as a by product, the framework provides the first university proof for some of the existing activation functions including Mish, SiLU, ELU, GELU, and etc. Fourth, it provides new proofs for most activation functions. Fifth, it discovers new activations with guaranteed universality property. Sixth, for a given activation and error tolerance, the framework provides precisely the architecture of the corresponding one-hidden neural network with predetermined number of neurons, and the values of weights/biases. Seventh, the framework allows us to abstractly present the first universal approximation with favorable non-asymptotic rate.
Model-Constrained Deep Learning Approaches for Inverse Problems
May 25, 2021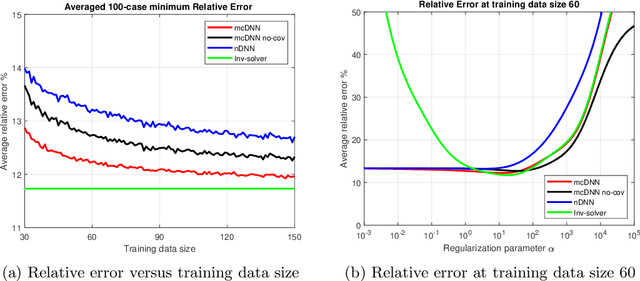
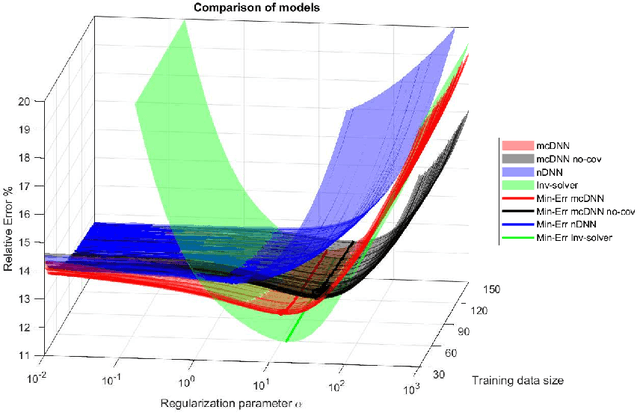

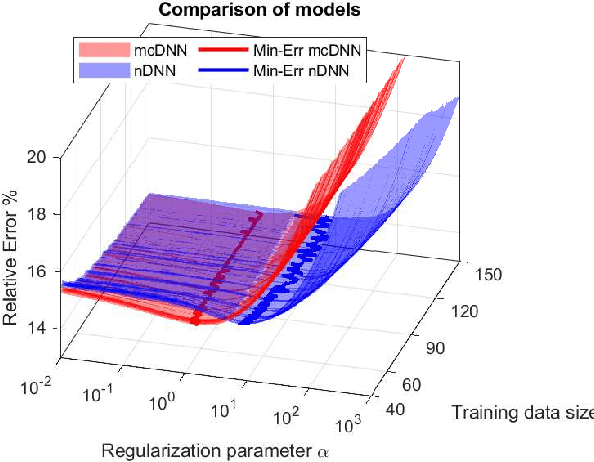
Abstract:Deep Learning (DL), in particular deep neural networks (DNN), by design is purely data-driven and in general does not require physics. This is the strength of DL but also one of its key limitations when applied to science and engineering problems in which underlying physical properties (such as stability, conservation, and positivity) and desired accuracy need to be achieved. DL methods in their original forms are not capable of respecting the underlying mathematical models or achieving desired accuracy even in big-data regimes. On the other hand, many data-driven science and engineering problems, such as inverse problems, typically have limited experimental or observational data, and DL would overfit the data in this case. Leveraging information encoded in the underlying mathematical models, we argue, not only compensates missing information in low data regimes but also provides opportunities to equip DL methods with the underlying physics and hence obtaining higher accuracy. This short communication introduces several model-constrained DL approaches (including both feed-forward DNN and autoencoders) that are capable of learning not only information hidden in the training data but also in the underlying mathematical models to solve inverse problems. We present and provide intuitions for our formulations for general nonlinear problems. For linear inverse problems and linear networks, the first order optimality conditions show that our model-constrained DL approaches can learn information encoded in the underlying mathematical models, and thus can produce consistent or equivalent inverse solutions, while naive purely data-based counterparts cannot.
Solving Forward and Inverse Problems Using Autoencoders
Jan 06, 2020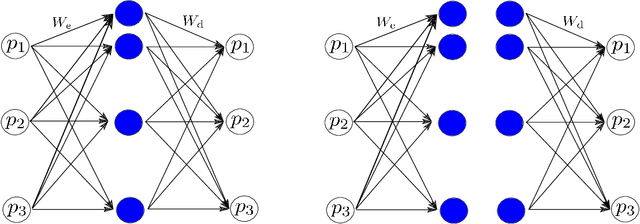


Abstract:This work develops a model-aware autoencoder networks as a new method for solving scientific forward and inverse problems. Autoencoders are unsupervised neural networks that are able to learn new representations of data through appropriately selected architecture and regularization. The resulting mappings to and from the latent representation can be used to encode and decode the data. In our work, we set the data space to be the parameter space of a parameter of interest we wish to invert for. Further, as a way to encode the underlying physical model into the autoencoder, we enforce the latent space of an autoencoder to be the space of observations of physically-governed phenomena. In doing so, we leverage the well known capability of a deep neural network as a universal function operator to simultaneously obtain both the parameter-to-observation and observation-to-parameter map. The results suggest that this simultaneous learning interacts synergistically to improve the the inversion capability of the autoencoder.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge