TAE: A Model-Constrained Tikhonov Autoencoder Approach for Forward and Inverse Problems

Efficient real-time solvers for forward and inverse problems are essential in engineering and science applications. Machine learning surrogate models have emerged as promising alternatives to traditional methods, offering substantially reduced computational time. Nevertheless, these models typically demand extensive training datasets to achieve robust generalization across diverse scenarios. While physics-based approaches can partially mitigate this data dependency and ensure physics-interpretable solutions, addressing scarce data regimes remains a challenge. Both purely data-driven and physics-based machine learning approaches demonstrate severe overfitting issues when trained with insufficient data. We propose a novel Tikhonov autoencoder model-constrained framework, called TAE, capable of learning both forward and inverse surrogate models using a single arbitrary observation sample. We develop comprehensive theoretical foundations including forward and inverse inference error bounds for the proposed approach for linear cases. For comparative analysis, we derive equivalent formulations for pure data-driven and model-constrained approach counterparts. At the heart of our approach is a data randomization strategy, which functions as a generative mechanism for exploring the training data space, enabling effective training of both forward and inverse surrogate models from a single observation, while regularizing the learning process. We validate our approach through extensive numerical experiments on two challenging inverse problems: 2D heat conductivity inversion and initial condition reconstruction for time-dependent 2D Navier-Stokes equations. Results demonstrate that TAE achieves accuracy comparable to traditional Tikhonov solvers and numerical forward solvers for both inverse and forward problems, respectively, while delivering orders of magnitude computational speedups.

Model-Constrained Deep Learning Approaches for Inverse Problems

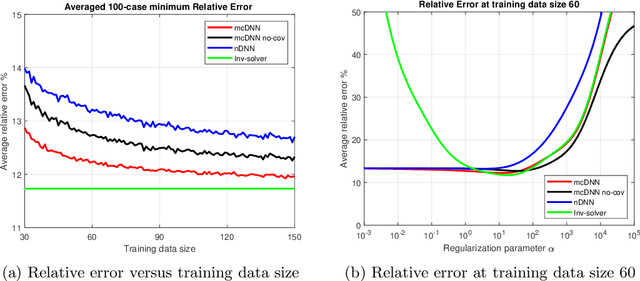
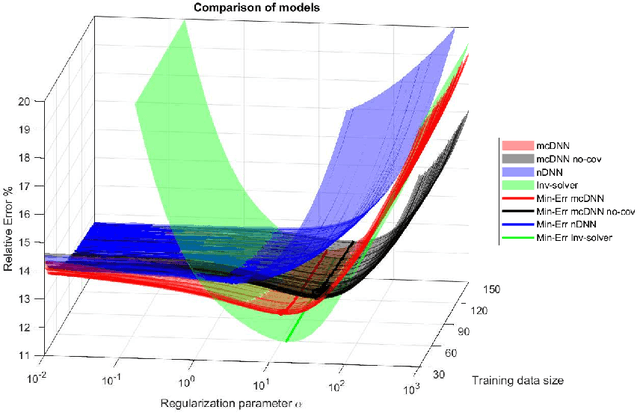
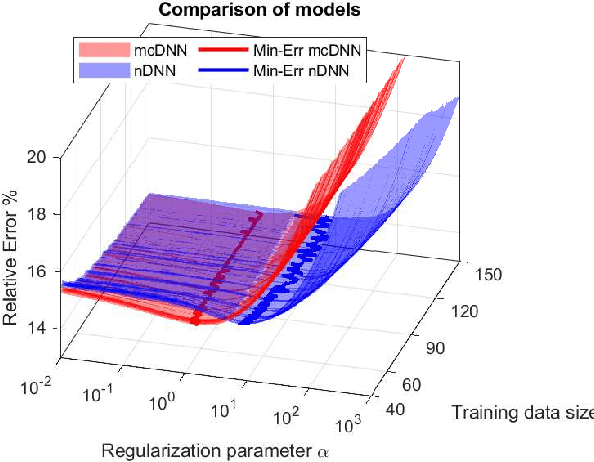
Deep Learning (DL), in particular deep neural networks (DNN), by design is purely data-driven and in general does not require physics. This is the strength of DL but also one of its key limitations when applied to science and engineering problems in which underlying physical properties (such as stability, conservation, and positivity) and desired accuracy need to be achieved. DL methods in their original forms are not capable of respecting the underlying mathematical models or achieving desired accuracy even in big-data regimes. On the other hand, many data-driven science and engineering problems, such as inverse problems, typically have limited experimental or observational data, and DL would overfit the data in this case. Leveraging information encoded in the underlying mathematical models, we argue, not only compensates missing information in low data regimes but also provides opportunities to equip DL methods with the underlying physics and hence obtaining higher accuracy. This short communication introduces several model-constrained DL approaches (including both feed-forward DNN and autoencoders) that are capable of learning not only information hidden in the training data but also in the underlying mathematical models to solve inverse problems. We present and provide intuitions for our formulations for general nonlinear problems. For linear inverse problems and linear networks, the first order optimality conditions show that our model-constrained DL approaches can learn information encoded in the underlying mathematical models, and thus can produce consistent or equivalent inverse solutions, while naive purely data-based counterparts cannot.