Robust, High-Precision GNSS Carrier-Phase Positioning with Visual-Inertial Fusion

Robust, high-precision global localization is fundamental to a wide range of outdoor robotics applications. Conventional fusion methods use low-accuracy pseudorange based GNSS measurements ($>>5m$ errors) and can only yield a coarse registration to the global earth-centered-earth-fixed (ECEF) frame. In this paper, we leverage high-precision GNSS carrier-phase positioning and aid it with local visual-inertial odometry (VIO) tracking using an extended Kalman filter (EKF) framework that better resolves the integer ambiguity concerned with GNSS carrier-phase. %to achieve centimeter-level accuracy in the ECEF frame. We also propose an algorithm for accurate GNSS-antenna-to-IMU extrinsics calibration to accurately align VIO to the ECEF frame. Together, our system achieves robust global positioning demonstrated by real-world hardware experiments in severely occluded urban canyons, and outperforms the state-of-the-art RTKLIB by a significant margin in terms of integer ambiguity solution fix rate and positioning RMSE accuracy.

Solving Forward and Inverse Problems Using Autoencoders

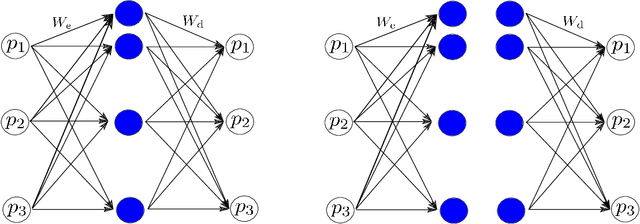
This work develops a model-aware autoencoder networks as a new method for solving scientific forward and inverse problems. Autoencoders are unsupervised neural networks that are able to learn new representations of data through appropriately selected architecture and regularization. The resulting mappings to and from the latent representation can be used to encode and decode the data. In our work, we set the data space to be the parameter space of a parameter of interest we wish to invert for. Further, as a way to encode the underlying physical model into the autoencoder, we enforce the latent space of an autoencoder to be the space of observations of physically-governed phenomena. In doing so, we leverage the well known capability of a deep neural network as a universal function operator to simultaneously obtain both the parameter-to-observation and observation-to-parameter map. The results suggest that this simultaneous learning interacts synergistically to improve the the inversion capability of the autoencoder.

Accelerating PDE-constrained Inverse Solutions with Deep Learning and Reduced Order Models

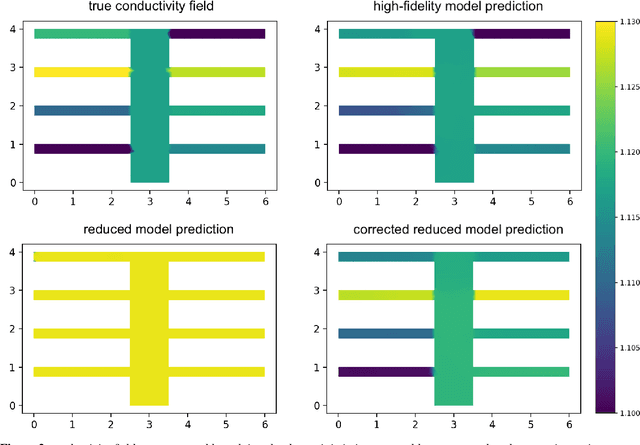
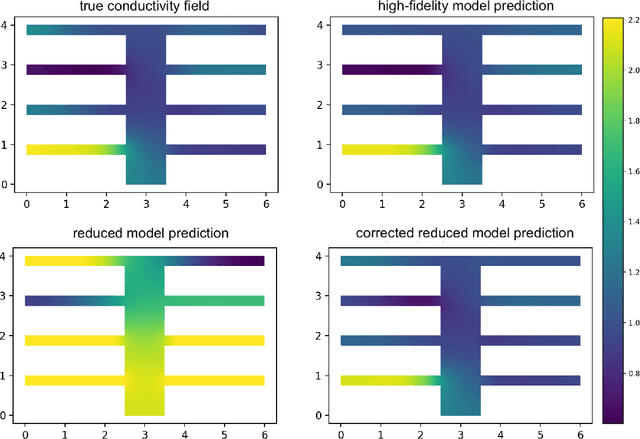
Inverse problems are pervasive mathematical methods in inferring knowledge from observational and experimental data by leveraging simulations and models. Unlike direct inference methods, inverse problem approaches typically require many forward model solves usually governed by Partial Differential Equations (PDEs). This a crucial bottleneck in determining the feasibility of such methods. While machine learning (ML) methods, such as deep neural networks (DNNs), can be employed to learn nonlinear forward models, designing a network architecture that preserves accuracy while generalizing to new parameter regimes is a daunting task. Furthermore, due to the computation-expensive nature of forward models, state-of-the-art black-box ML methods would require an unrealistic amount of work in order to obtain an accurate surrogate model. On the other hand, standard Reduced-Order Models (ROMs) accurately capture supposedly important physics of the forward model in the reduced subspaces, but otherwise could be inaccurate elsewhere. In this paper, we propose to enlarge the validity of ROMs and hence improve the accuracy outside the reduced subspaces by incorporating a data-driven ML technique. In particular, we focus on a goal-oriented approach that substantially improves the accuracy of reduced models by learning the error between the forward model and the ROM outputs. Once an ML-enhanced ROM is constructed it can accelerate the performance of solving many-query problems in parametrized forward and inverse problems. Numerical results for inverse problems governed by elliptic PDEs and parametrized neutron transport equations will be presented to support our approach.