Accelerating Training in Artificial Neural Networks with Dynamic Mode Decomposition

Training of deep neural networks (DNNs) frequently involves optimizing several millions or even billions of parameters. Even with modern computing architectures, the computational expense of DNN training can inhibit, for instance, network architecture design optimization, hyper-parameter studies, and integration into scientific research cycles. The key factor limiting performance is that both the feed-forward evaluation and the back-propagation rule are needed for each weight during optimization in the update rule. In this work, we propose a method to decouple the evaluation of the update rule at each weight. At first, Proper Orthogonal Decomposition (POD) is used to identify a current estimate of the principal directions of evolution of weights per layer during training based on the evolution observed with a few backpropagation steps. Then, Dynamic Mode Decomposition (DMD) is used to learn the dynamics of the evolution of the weights in each layer according to these principal directions. The DMD model is used to evaluate an approximate converged state when training the ANN. Afterward, some number of backpropagation steps are performed, starting from the DMD estimates, leading to an update to the principal directions and DMD model. This iterative process is repeated until convergence. By fine-tuning the number of backpropagation steps used for each DMD model estimation, a significant reduction in the number of operations required to train the neural networks can be achieved. In this paper, the DMD acceleration method will be explained in detail, along with the theoretical justification for the acceleration provided by DMD. This method is illustrated using a regression problem of key interest for the scientific machine learning community: the prediction of a pollutant concentration field in a diffusion, advection, reaction problem.

Accelerating PDE-constrained Inverse Solutions with Deep Learning and Reduced Order Models

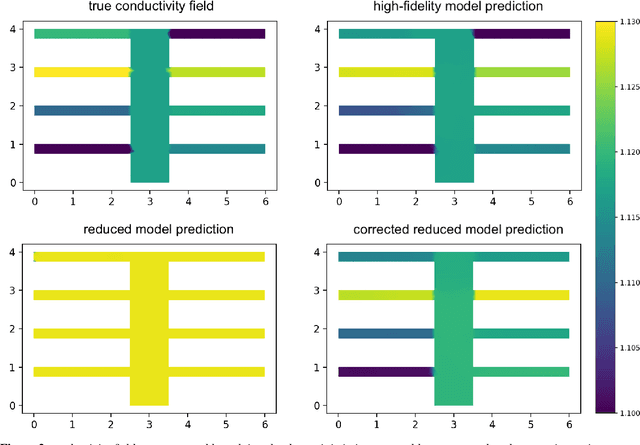
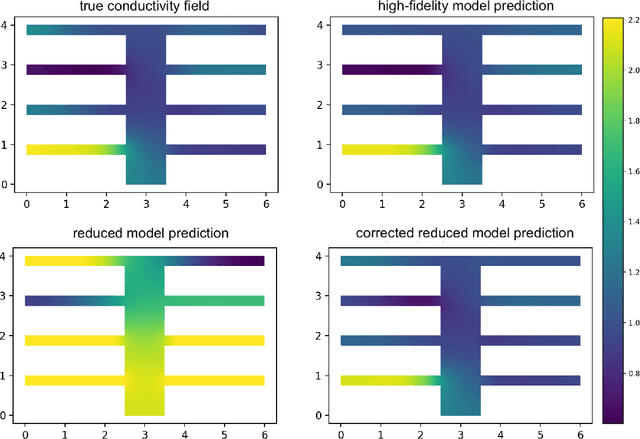
Inverse problems are pervasive mathematical methods in inferring knowledge from observational and experimental data by leveraging simulations and models. Unlike direct inference methods, inverse problem approaches typically require many forward model solves usually governed by Partial Differential Equations (PDEs). This a crucial bottleneck in determining the feasibility of such methods. While machine learning (ML) methods, such as deep neural networks (DNNs), can be employed to learn nonlinear forward models, designing a network architecture that preserves accuracy while generalizing to new parameter regimes is a daunting task. Furthermore, due to the computation-expensive nature of forward models, state-of-the-art black-box ML methods would require an unrealistic amount of work in order to obtain an accurate surrogate model. On the other hand, standard Reduced-Order Models (ROMs) accurately capture supposedly important physics of the forward model in the reduced subspaces, but otherwise could be inaccurate elsewhere. In this paper, we propose to enlarge the validity of ROMs and hence improve the accuracy outside the reduced subspaces by incorporating a data-driven ML technique. In particular, we focus on a goal-oriented approach that substantially improves the accuracy of reduced models by learning the error between the forward model and the ROM outputs. Once an ML-enhanced ROM is constructed it can accelerate the performance of solving many-query problems in parametrized forward and inverse problems. Numerical results for inverse problems governed by elliptic PDEs and parametrized neutron transport equations will be presented to support our approach.