A Unified and Constructive Framework for the Universality of Neural Networks

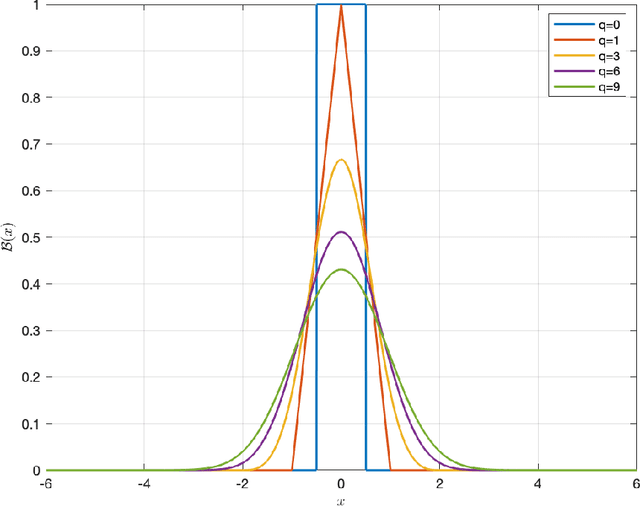
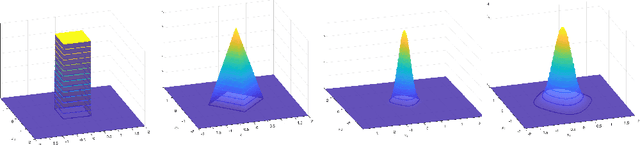
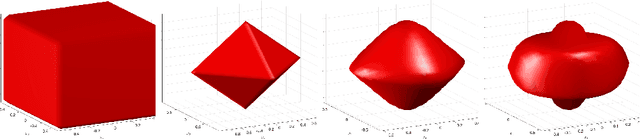
One of the reasons why many neural networks are capable of replicating complicated tasks or functions is their universal property. Though the past few decades have seen tremendous advances in theories of neural networks, a single constructive framework for neural network universality remains unavailable. This paper is an effort to provide a unified and constructive framework for the universality of a large class of activations including most of existing ones. At the heart of the framework is the concept of neural network approximate identity (nAI). The main result is: {\em any nAI activation function is universal}. It turns out that most of existing activations are nAI, and thus universal in the space of continuous functions on compacta. The framework has the following main properties. First, it is constructive with elementary means from functional analysis, probability theory, and numerical analysis. Second, it is the first unified attempt that is valid for most of existing activations. Third, as a by product, the framework provides the first university proof for some of the existing activation functions including Mish, SiLU, ELU, GELU, and etc. Fourth, it provides new proofs for most activation functions. Fifth, it discovers new activations with guaranteed universality property. Sixth, for a given activation and error tolerance, the framework provides precisely the architecture of the corresponding one-hidden neural network with predetermined number of neurons, and the values of weights/biases. Seventh, the framework allows us to abstractly present the first universal approximation with favorable non-asymptotic rate.