Deep learning-based fast solver of the shallow water equations
Paper and Code
Nov 23, 2021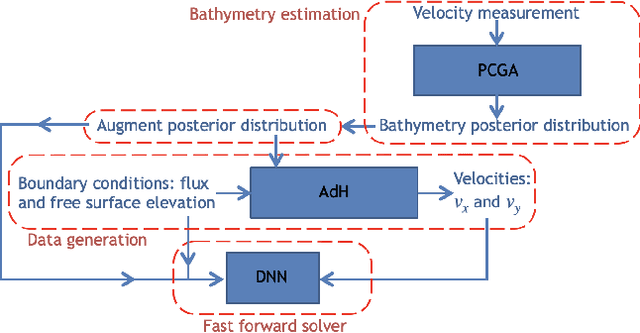
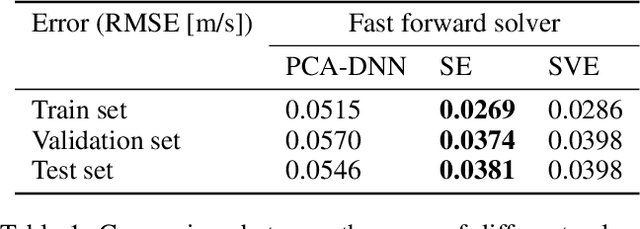
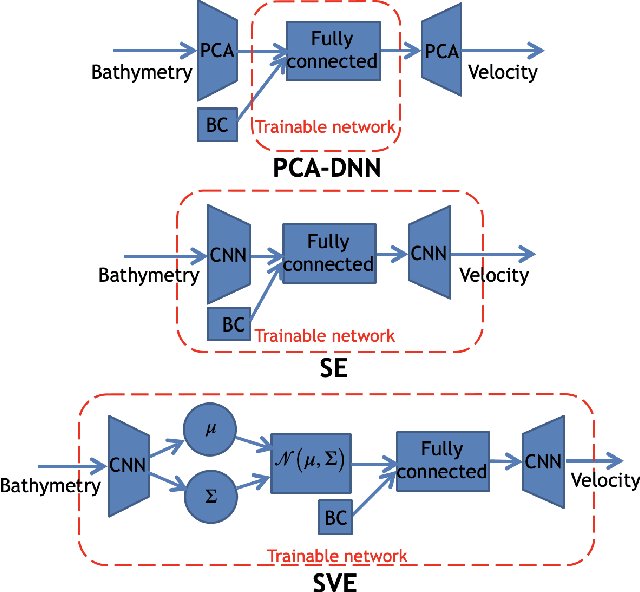

Fast and reliable prediction of river flow velocities is important in many applications, including flood risk management. The shallow water equations (SWEs) are commonly used for this purpose. However, traditional numerical solvers of the SWEs are computationally expensive and require high-resolution riverbed profile measurement (bathymetry). In this work, we propose a two-stage process in which, first, using the principal component geostatistical approach (PCGA) we estimate the probability density function of the bathymetry from flow velocity measurements, and then use machine learning (ML) algorithms to obtain a fast solver for the SWEs. The fast solver uses realizations from the posterior bathymetry distribution and takes as input the prescribed range of BCs. The first stage allows us to predict flow velocities without direct measurement of the bathymetry. Furthermore, we augment the bathymetry posterior distribution to a more general class of distributions before providing them as inputs to ML algorithm in the second stage. This allows the solver to incorporate future direct bathymetry measurements into the flow velocity prediction for improved accuracy, even if the bathymetry changes over time compared to its original indirect estimation. We propose and benchmark three different solvers, referred to as PCA-DNN (principal component analysis-deep neural network), SE (supervised encoder), and SVE (supervised variational encoder), and validate them on the Savannah river, Augusta, GA. Our results show that the fast solvers are capable of predicting flow velocities for different bathymetry and BCs with good accuracy, at a computational cost that is significantly lower than the cost of solving the full boundary value problem with traditional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge