AutoSciLab: A Self-Driving Laboratory For Interpretable Scientific Discovery

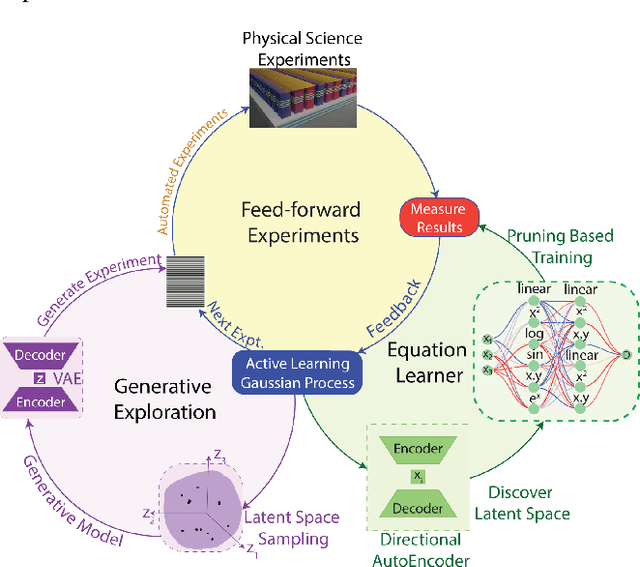
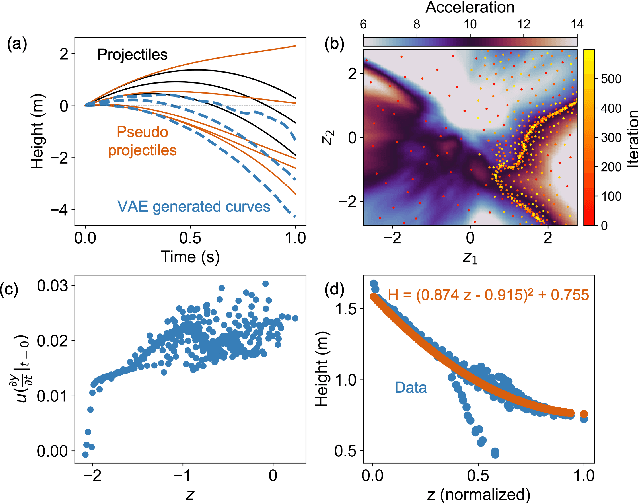
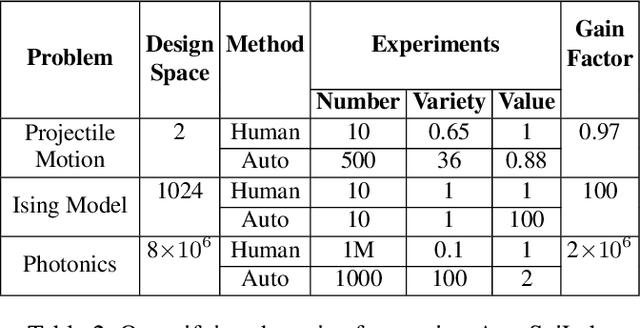
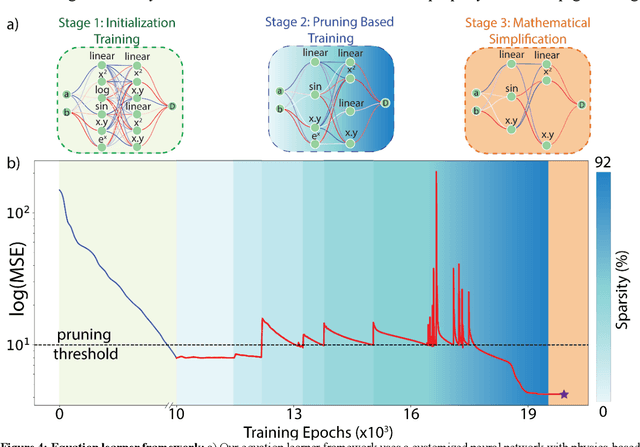
Advances in robotic control and sensing have propelled the rise of automated scientific laboratories capable of high-throughput experiments. However, automated scientific laboratories are currently limited by human intuition in their ability to efficiently design and interpret experiments in high-dimensional spaces, throttling scientific discovery. We present AutoSciLab, a machine learning framework for driving autonomous scientific experiments, forming a surrogate researcher purposed for scientific discovery in high-dimensional spaces. AutoSciLab autonomously follows the scientific method in four steps: (i) generating high-dimensional experiments (x \in R^D) using a variational autoencoder (ii) selecting optimal experiments by forming hypotheses using active learning (iii) distilling the experimental results to discover relevant low-dimensional latent variables (z \in R^d, with d << D) with a 'directional autoencoder' and (iv) learning a human interpretable equation connecting the discovered latent variables with a quantity of interest (y = f(z)), using a neural network equation learner. We validate the generalizability of AutoSciLab by rediscovering a) the principles of projectile motion and b) the phase transitions within the spin-states of the Ising model (NP-hard problem). Applying our framework to an open-ended nanophotonics challenge, AutoSciLab uncovers a fundamentally novel method for directing incoherent light emission that surpasses the current state-of-the-art (Iyer et al. 2023b, 2020).

Self-driving lab discovers principles for steering spontaneous emission

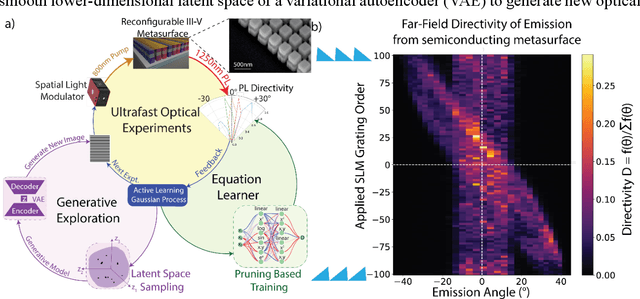
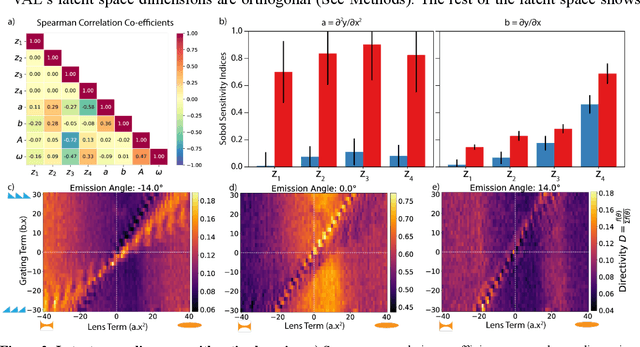
We developed an autonomous experimentation platform to accelerate interpretable scientific discovery in ultrafast nanophotonics, targeting a novel method to steer spontaneous emission from reconfigurable semiconductor metasurfaces. Controlling spontaneous emission is crucial for clean-energy solutions in illumination, thermal radiation engineering, and remote sensing. Despite the potential of reconfigurable semiconductor metasurfaces with embedded sources for spatiotemporal control, achieving arbitrary far-field control remains challenging. Here, we present a self-driving lab (SDL) platform that addresses this challenge by discovering the governing equations for predicting the far-field emission profile from light-emitting metasurfaces. We discover that both the spatial gradient (grating-like) and the curvature (lens-like) of the local refractive index are key factors in steering spontaneous emission. The SDL employs a machine-learning framework comprising: (1) a variational autoencoder for generating complex spatial refractive index profiles, (2) an active learning agent for guiding experiments with real-time closed-loop feedback, and (3) a neural network-based equation learner to uncover structure-property relationships. The SDL demonstrated a four-fold enhancement in peak emission directivity (up to 77%) over a 72{\deg} field of view within ~300 experiments. Our findings reveal that combinations of positive gratings and lenses are as effective as negative lenses and gratings for all emission angles, offering a novel strategy for controlling spontaneous emission beyond conventional Fourier optics.

Rethinking materials simulations: Blending direct numerical simulations with neural operators

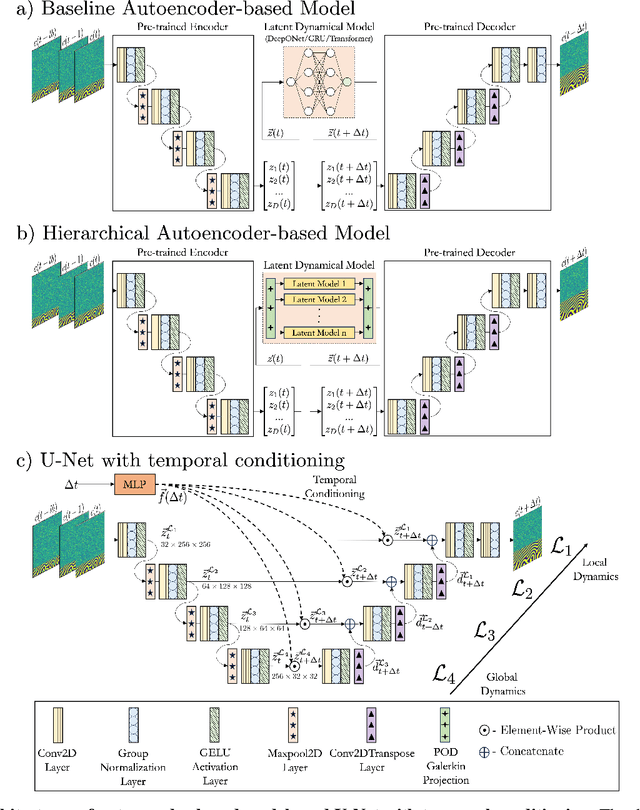
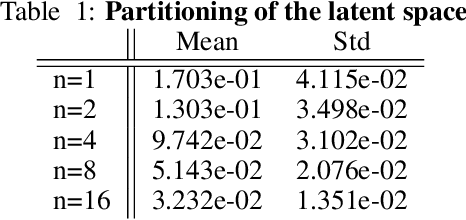
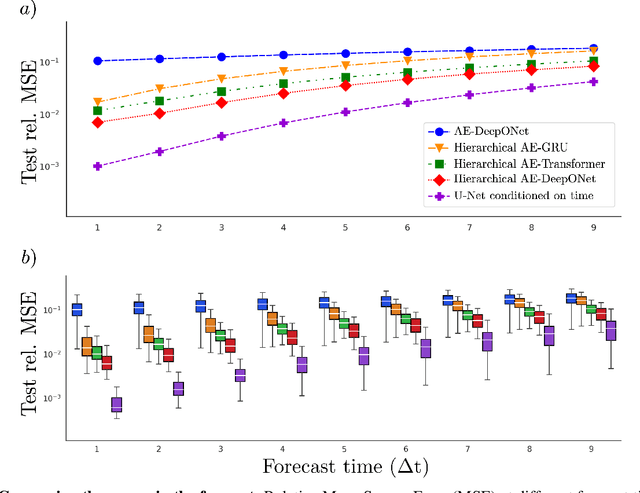
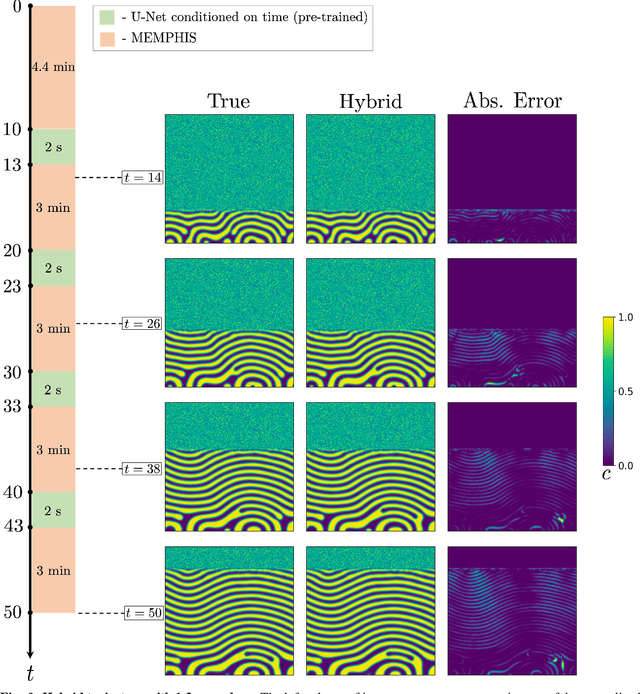
Direct numerical simulations (DNS) are accurate but computationally expensive for predicting materials evolution across timescales, due to the complexity of the underlying evolution equations, the nature of multiscale spatio-temporal interactions, and the need to reach long-time integration. We develop a new method that blends numerical solvers with neural operators to accelerate such simulations. This methodology is based on the integration of a community numerical solver with a U-Net neural operator, enhanced by a temporal-conditioning mechanism that enables accurate extrapolation and efficient time-to-solution predictions of the dynamics. We demonstrate the effectiveness of this framework on simulations of microstructure evolution during physical vapor deposition modeled via the phase-field method. Such simulations exhibit high spatial gradients due to the co-evolution of different material phases with simultaneous slow and fast materials dynamics. We establish accurate extrapolation of the coupled solver with up to 16.5$\times$ speed-up compared to DNS. This methodology is generalizable to a broad range of evolutionary models, from solid mechanics, to fluid dynamics, geophysics, climate, and more.

Learning two-phase microstructure evolution using neural operators and autoencoder architectures

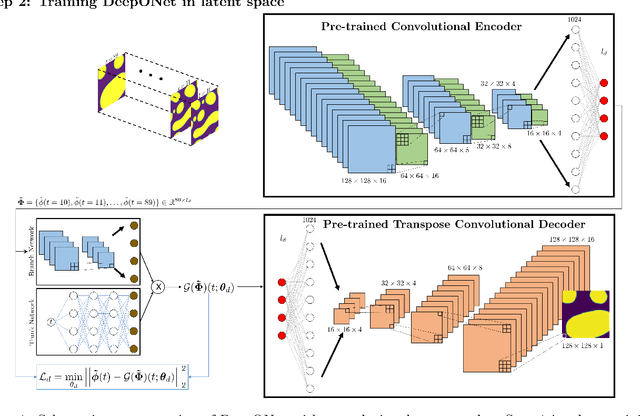
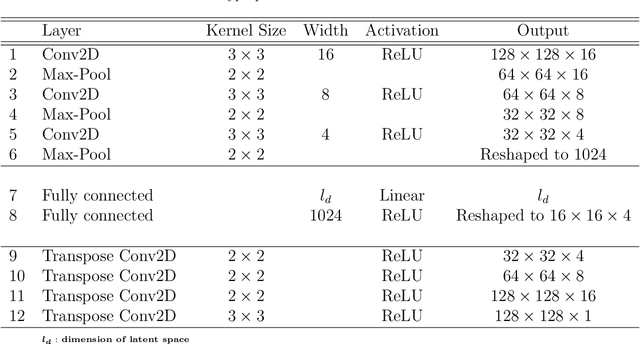
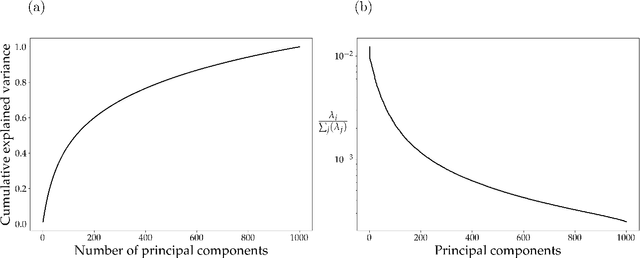
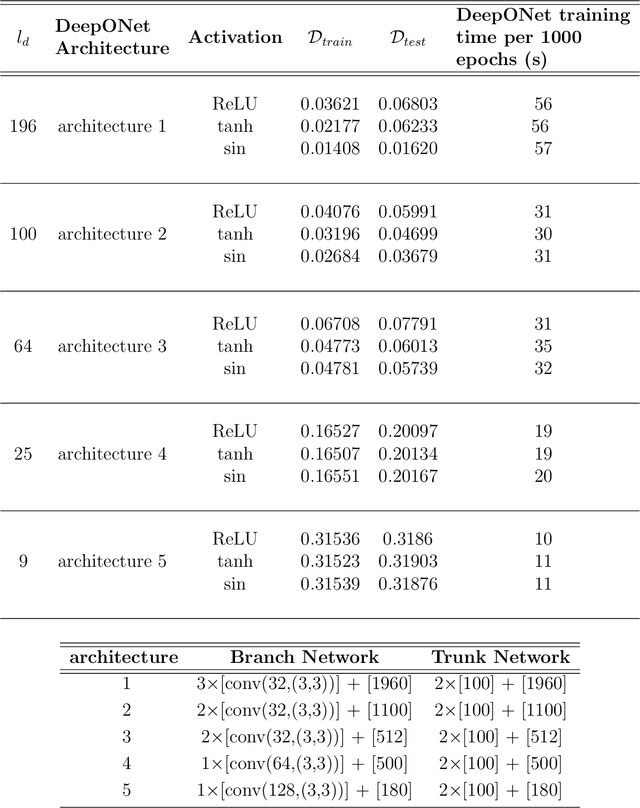
Phase-field modeling is an effective mesoscale method for capturing the evolution dynamics of materials, e.g., in spinodal decomposition of a two-phase mixture. However, the accuracy of high-fidelity phase field models comes at a substantial computational cost. Hence, fast and generalizable surrogate models are needed to alleviate the cost in computationally taxing processes such as in optimization and design of materials. The intrinsic discontinuous nature of the physical phenomena incurred by the presence of sharp phase boundaries makes the training of the surrogate model cumbersome. We develop a new framework that integrates a convolutional autoencoder architecture with a deep neural operator (DeepONet) to learn the dynamic evolution of a two-phase mixture. We utilize the convolutional autoencoder to provide a compact representation of the microstructure data in a low-dimensional latent space. DeepONet, which consists of two sub-networks, one for encoding the input function at a fixed number of sensors locations (branch net) and another for encoding the locations for the output functions (trunk net), learns the mesoscale dynamics of the microstructure evolution in the latent space. The decoder part of the convolutional autoencoder can then reconstruct the time-evolved microstructure from the DeepONet predictions. The result is an efficient and accurate accelerated phase-field framework that outperforms other neural-network-based approaches while at the same time being robust to noisy inputs.

Inferring topological transitions in pattern-forming processes with self-supervised learning

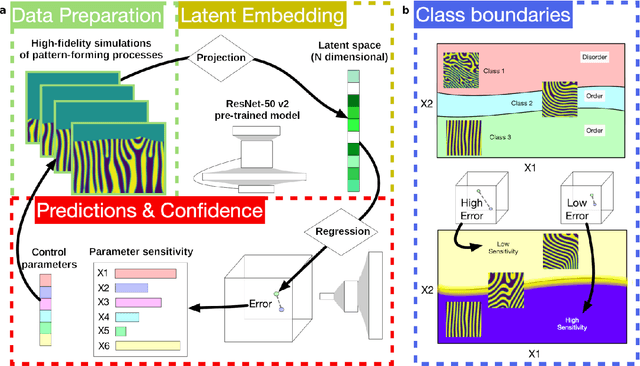
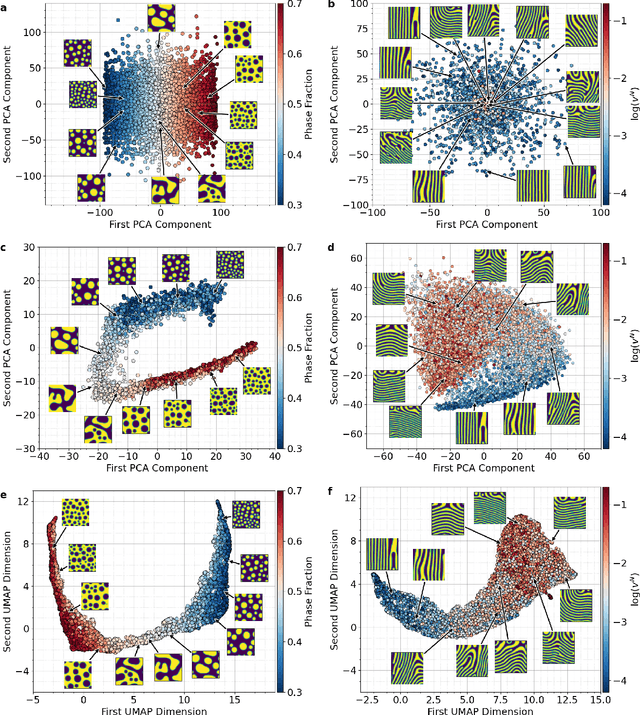
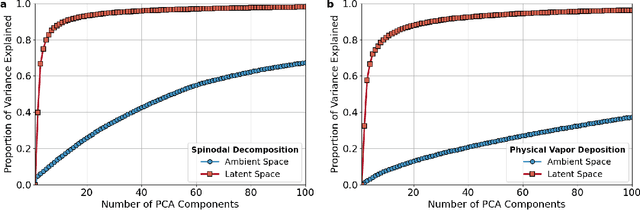
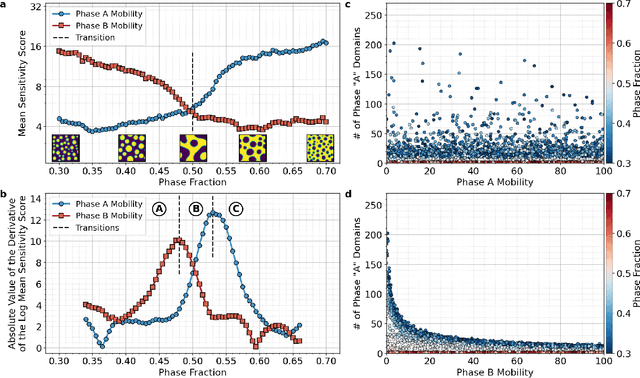
The identification and classification of transitions in topological and microstructural regimes in pattern-forming processes is critical for understanding and fabricating microstructurally precise novel materials in many application domains. Unfortunately, relevant microstructure transitions may depend on process parameters in subtle and complex ways that are not captured by the classic theory of phase transition. While supervised machine learning methods may be useful for identifying transition regimes, they need labels which require prior knowledge of order parameters or relevant structures. Motivated by the universality principle for dynamical systems, we instead use a self-supervised approach to solve the inverse problem of predicting process parameters from observed microstructures using neural networks. This approach does not require labeled data about the target task of predicting microstructure transitions. We show that the difficulty of performing this prediction task is related to the goal of discovering microstructure regimes, because qualitative changes in microstructural patterns correspond to changes in uncertainty for our self-supervised prediction problem. We demonstrate the value of our approach by automatically discovering transitions in microstructural regimes in two distinct pattern-forming processes: the spinodal decomposition of a two-phase mixture and the formation of concentration modulations of binary alloys during physical vapor deposition of thin films. This approach opens a promising path forward for discovering and understanding unseen or hard-to-detect transition regimes, and ultimately for controlling complex pattern-forming processes.