Inferring topological transitions in pattern-forming processes with self-supervised learning

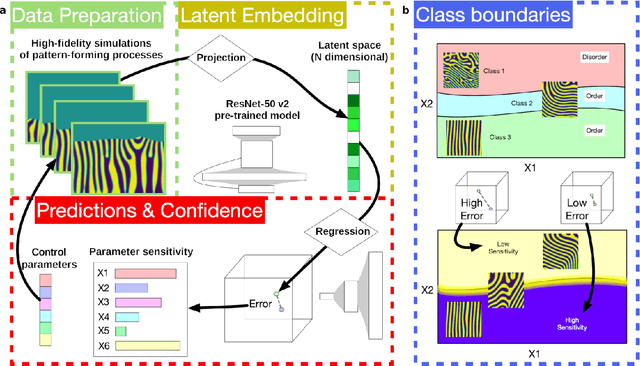
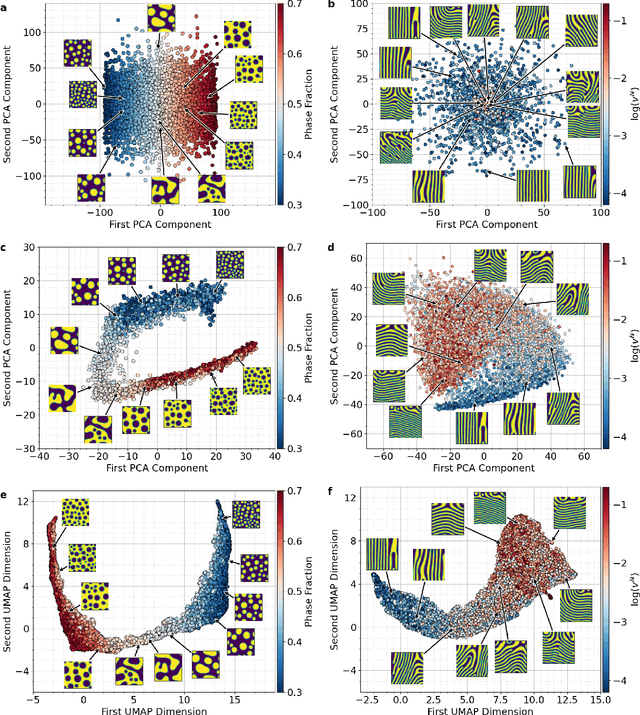
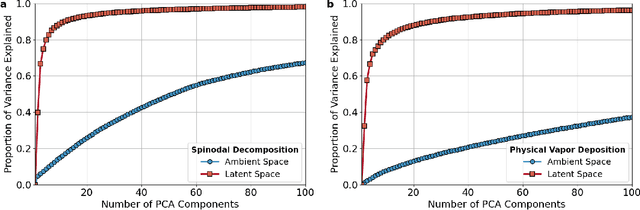
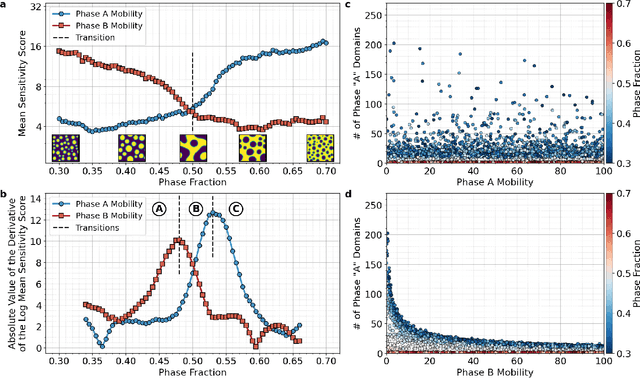
The identification and classification of transitions in topological and microstructural regimes in pattern-forming processes is critical for understanding and fabricating microstructurally precise novel materials in many application domains. Unfortunately, relevant microstructure transitions may depend on process parameters in subtle and complex ways that are not captured by the classic theory of phase transition. While supervised machine learning methods may be useful for identifying transition regimes, they need labels which require prior knowledge of order parameters or relevant structures. Motivated by the universality principle for dynamical systems, we instead use a self-supervised approach to solve the inverse problem of predicting process parameters from observed microstructures using neural networks. This approach does not require labeled data about the target task of predicting microstructure transitions. We show that the difficulty of performing this prediction task is related to the goal of discovering microstructure regimes, because qualitative changes in microstructural patterns correspond to changes in uncertainty for our self-supervised prediction problem. We demonstrate the value of our approach by automatically discovering transitions in microstructural regimes in two distinct pattern-forming processes: the spinodal decomposition of a two-phase mixture and the formation of concentration modulations of binary alloys during physical vapor deposition of thin films. This approach opens a promising path forward for discovering and understanding unseen or hard-to-detect transition regimes, and ultimately for controlling complex pattern-forming processes.