Probabilistic partition of unity networks for high-dimensional regression problems
Paper and Code
Oct 06, 2022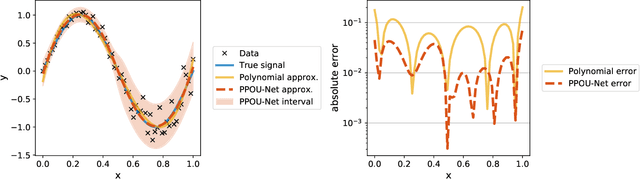
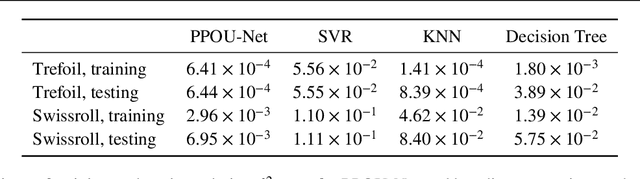
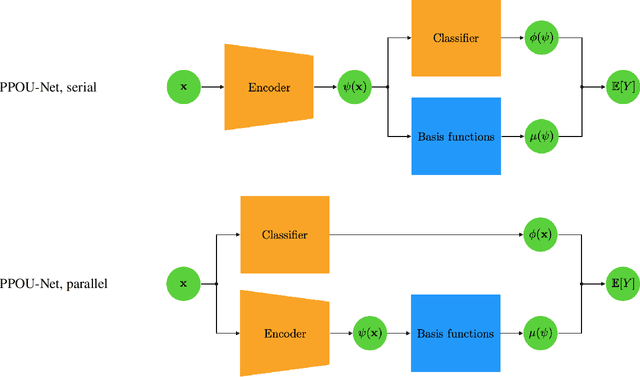
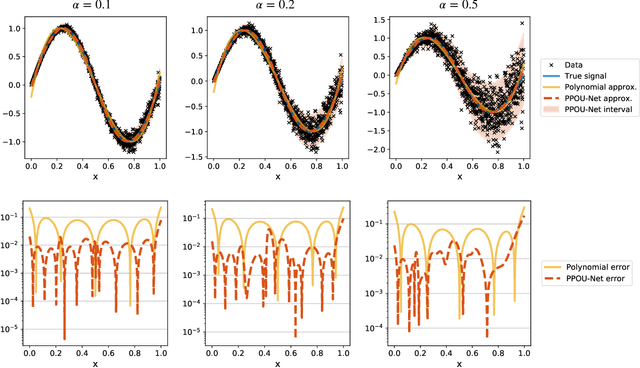
We explore the probabilistic partition of unity network (PPOU-Net) model in the context of high-dimensional regression problems. With the PPOU-Nets, the target function for any given input is approximated by a mixture of experts model, where each cluster is associated with a fixed-degree polynomial. The weights of the clusters are determined by a DNN that defines a partition of unity. The weighted average of the polynomials approximates the target function and produces uncertainty quantification naturally. Our training strategy leverages automatic differentiation and the expectation maximization (EM) algorithm. During the training, we (i) apply gradient descent to update the DNN coefficients; (ii) update the polynomial coefficients using weighted least-squares solves; and (iii) compute the variance of each cluster according to a closed-form formula derived from the EM algorithm. The PPOU-Nets consistently outperform the baseline fully-connected neural networks of comparable sizes in numerical experiments of various data dimensions. We also explore the proposed model in applications of quantum computing, where the PPOU-Nets act as surrogate models for cost landscapes associated with variational quantum circuits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge