Parameter-varying neural ordinary differential equations with partition-of-unity networks
Paper and Code
Oct 01, 2022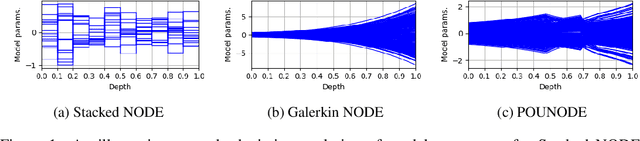



In this study, we propose parameter-varying neural ordinary differential equations (NODEs) where the evolution of model parameters is represented by partition-of-unity networks (POUNets), a mixture of experts architecture. The proposed variant of NODEs, synthesized with POUNets, learn a meshfree partition of space and represent the evolution of ODE parameters using sets of polynomials associated to each partition. We demonstrate the effectiveness of the proposed method for three important tasks: data-driven dynamics modeling of (1) hybrid systems, (2) switching linear dynamical systems, and (3) latent dynamics for dynamical systems with varying external forcing.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge