Nonlocal Attention Operator: Materializing Hidden Knowledge Towards Interpretable Physics Discovery
Paper and Code
Aug 14, 2024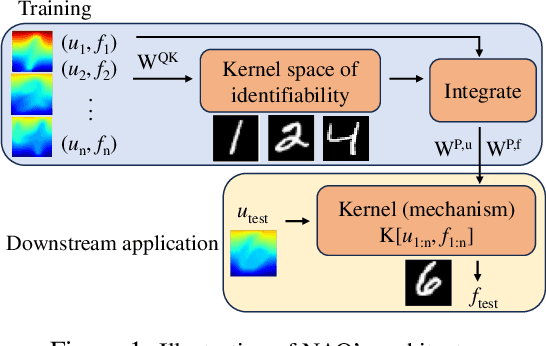
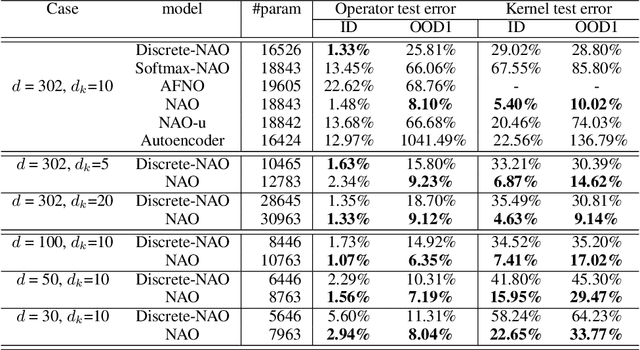
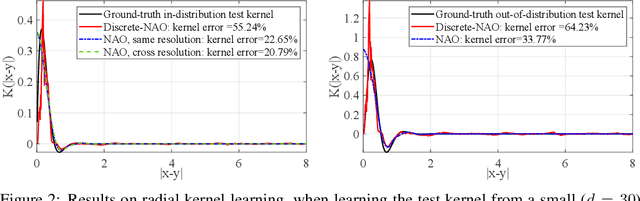
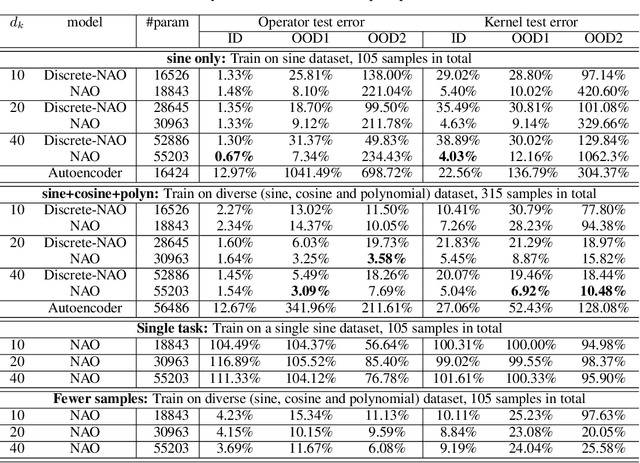
Despite the recent popularity of attention-based neural architectures in core AI fields like natural language processing (NLP) and computer vision (CV), their potential in modeling complex physical systems remains under-explored. Learning problems in physical systems are often characterized as discovering operators that map between function spaces based on a few instances of function pairs. This task frequently presents a severely ill-posed PDE inverse problem. In this work, we propose a novel neural operator architecture based on the attention mechanism, which we coin Nonlocal Attention Operator (NAO), and explore its capability towards developing a foundation physical model. In particular, we show that the attention mechanism is equivalent to a double integral operator that enables nonlocal interactions among spatial tokens, with a data-dependent kernel characterizing the inverse mapping from data to the hidden parameter field of the underlying operator. As such, the attention mechanism extracts global prior information from training data generated by multiple systems, and suggests the exploratory space in the form of a nonlinear kernel map. Consequently, NAO can address ill-posedness and rank deficiency in inverse PDE problems by encoding regularization and achieving generalizability. We empirically demonstrate the advantages of NAO over baseline neural models in terms of generalizability to unseen data resolutions and system states. Our work not only suggests a novel neural operator architecture for learning interpretable foundation models of physical systems, but also offers a new perspective towards understanding the attention mechanism.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge