Tackling the Curse of Dimensionality in Fractional and Tempered Fractional PDEs with Physics-Informed Neural Networks

Fractional and tempered fractional partial differential equations (PDEs) are effective models of long-range interactions, anomalous diffusion, and non-local effects. Traditional numerical methods for these problems are mesh-based, thus struggling with the curse of dimensionality (CoD). Physics-informed neural networks (PINNs) offer a promising solution due to their universal approximation, generalization ability, and mesh-free training. In principle, Monte Carlo fractional PINN (MC-fPINN) estimates fractional derivatives using Monte Carlo methods and thus could lift CoD. However, this may cause significant variance and errors, hence affecting convergence; in addition, MC-fPINN is sensitive to hyperparameters. In general, numerical methods and specifically PINNs for tempered fractional PDEs are under-developed. Herein, we extend MC-fPINN to tempered fractional PDEs to address these issues, resulting in the Monte Carlo tempered fractional PINN (MC-tfPINN). To reduce possible high variance and errors from Monte Carlo sampling, we replace the one-dimensional (1D) Monte Carlo with 1D Gaussian quadrature, applicable to both MC-fPINN and MC-tfPINN. We validate our methods on various forward and inverse problems of fractional and tempered fractional PDEs, scaling up to 100,000 dimensions. Our improved MC-fPINN/MC-tfPINN using quadrature consistently outperforms the original versions in accuracy and convergence speed in very high dimensions.

Score-fPINN: Fractional Score-Based Physics-Informed Neural Networks for High-Dimensional Fokker-Planck-Levy Equations

We introduce an innovative approach for solving high-dimensional Fokker-Planck-L\'evy (FPL) equations in modeling non-Brownian processes across disciplines such as physics, finance, and ecology. We utilize a fractional score function and Physical-informed neural networks (PINN) to lift the curse of dimensionality (CoD) and alleviate numerical overflow from exponentially decaying solutions with dimensions. The introduction of a fractional score function allows us to transform the FPL equation into a second-order partial differential equation without fractional Laplacian and thus can be readily solved with standard physics-informed neural networks (PINNs). We propose two methods to obtain a fractional score function: fractional score matching (FSM) and score-fPINN for fitting the fractional score function. While FSM is more cost-effective, it relies on known conditional distributions. On the other hand, score-fPINN is independent of specific stochastic differential equations (SDEs) but requires evaluating the PINN model's derivatives, which may be more costly. We conduct our experiments on various SDEs and demonstrate numerical stability and effectiveness of our method in dealing with high-dimensional problems, marking a significant advancement in addressing the CoD in FPL equations.

Transformers as Neural Operators for Solutions of Differential Equations with Finite Regularity

Neural operator learning models have emerged as very effective surrogates in data-driven methods for partial differential equations (PDEs) across different applications from computational science and engineering. Such operator learning models not only predict particular instances of a physical or biological system in real-time but also forecast classes of solutions corresponding to a distribution of initial and boundary conditions or forcing terms. % DeepONet is the first neural operator model and has been tested extensively for a broad class of solutions, including Riemann problems. Transformers have not been used in that capacity, and specifically, they have not been tested for solutions of PDEs with low regularity. % In this work, we first establish the theoretical groundwork that transformers possess the universal approximation property as operator learning models. We then apply transformers to forecast solutions of diverse dynamical systems with solutions of finite regularity for a plurality of initial conditions and forcing terms. In particular, we consider three examples: the Izhikevich neuron model, the tempered fractional-order Leaky Integrate-and-Fire (LIF) model, and the one-dimensional Euler equation Riemann problem. For the latter problem, we also compare with variants of DeepONet, and we find that transformers outperform DeepONet in accuracy but they are computationally more expensive.

Two-scale Neural Networks for Partial Differential Equations with Small Parameters

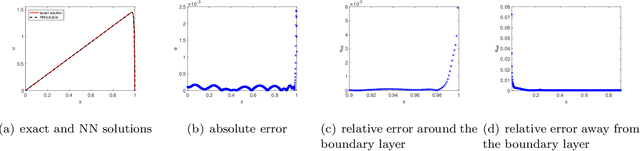
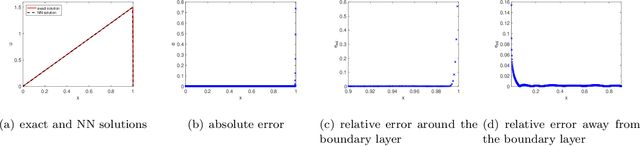
We propose a two-scale neural network method for solving partial differential equations (PDEs) with small parameters using physics-informed neural networks (PINNs). We directly incorporate the small parameters into the architecture of neural networks. The proposed method enables solving PDEs with small parameters in a simple fashion, without adding Fourier features or other computationally taxing searches of truncation parameters. Various numerical examples demonstrate reasonable accuracy in capturing features of large derivatives in the solutions caused by small parameters.

Score-Based Physics-Informed Neural Networks for High-Dimensional Fokker-Planck Equations

The Fokker-Planck (FP) equation is a foundational PDE in stochastic processes. However, curse of dimensionality (CoD) poses challenge when dealing with high-dimensional FP PDEs. Although Monte Carlo and vanilla Physics-Informed Neural Networks (PINNs) have shown the potential to tackle CoD, both methods exhibit numerical errors in high dimensions when dealing with the probability density function (PDF) associated with Brownian motion. The point-wise PDF values tend to decrease exponentially as dimension increases, surpassing the precision of numerical simulations and resulting in substantial errors. Moreover, due to its massive sampling, Monte Carlo fails to offer fast sampling. Modeling the logarithm likelihood (LL) via vanilla PINNs transforms the FP equation into a difficult HJB equation, whose error grows rapidly with dimension. To this end, we propose a novel approach utilizing a score-based solver to fit the score function in SDEs. The score function, defined as the gradient of the LL, plays a fundamental role in inferring LL and PDF and enables fast SDE sampling. Three fitting methods, Score Matching (SM), Sliced SM (SSM), and Score-PINN, are introduced. The proposed score-based SDE solver operates in two stages: first, employing SM, SSM, or Score-PINN to acquire the score; and second, solving the LL via an ODE using the obtained score. Comparative evaluations across these methods showcase varying trade-offs. The proposed method is evaluated across diverse SDEs, including anisotropic OU processes, geometric Brownian, and Brownian with varying eigenspace. We also test various distributions, including Gaussian, Log-normal, Laplace, and Cauchy. The numerical results demonstrate the score-based SDE solver's stability, speed, and performance across different settings, solidifying its potential as a solution to CoD for high-dimensional FP equations.

Peridynamic Neural Operators: A Data-Driven Nonlocal Constitutive Model for Complex Material Responses

Neural operators, which can act as implicit solution operators of hidden governing equations, have recently become popular tools for learning the responses of complex real-world physical systems. Nevertheless, most neural operator applications have thus far been data-driven and neglect the intrinsic preservation of fundamental physical laws in data. In this work, we introduce a novel integral neural operator architecture called the Peridynamic Neural Operator (PNO) that learns a nonlocal constitutive law from data. This neural operator provides a forward model in the form of state-based peridynamics, with objectivity and momentum balance laws automatically guaranteed. As applications, we demonstrate the expressivity and efficacy of our model in learning complex material behaviors from both synthetic and experimental data sets. We show that, owing to its ability to capture complex responses, our learned neural operator achieves improved accuracy and efficiency compared to baseline models that use predefined constitutive laws. Moreover, by preserving the essential physical laws within the neural network architecture, the PNO is robust in treating noisy data. The method shows generalizability to different domain configurations, external loadings, and discretizations.

hp-VPINNs: Variational Physics-Informed Neural Networks With Domain Decomposition

We formulate a general framework for hp-variational physics-informed neural networks (hp-VPINNs) based on the nonlinear approximation of shallow and deep neural networks and hp-refinement via domain decomposition and projection onto space of high-order polynomials. The trial space is the space of neural network, which is defined globally over the whole computational domain, while the test space contains the piecewise polynomials. Specifically in this study, the hp-refinement corresponds to a global approximation with local learning algorithm that can efficiently localize the network parameter optimization. We demonstrate the advantages of hp-VPINNs in accuracy and training cost for several numerical examples of function approximation and solving differential equations.

Knowledge-guided Semantic Computing Network

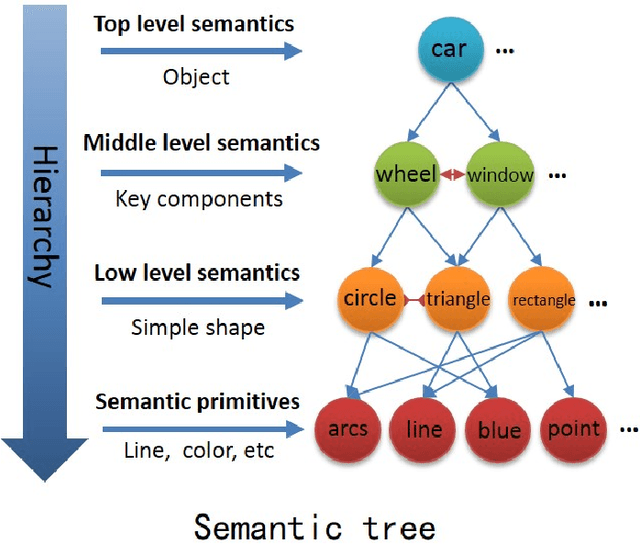
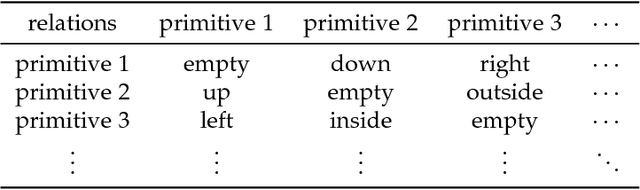
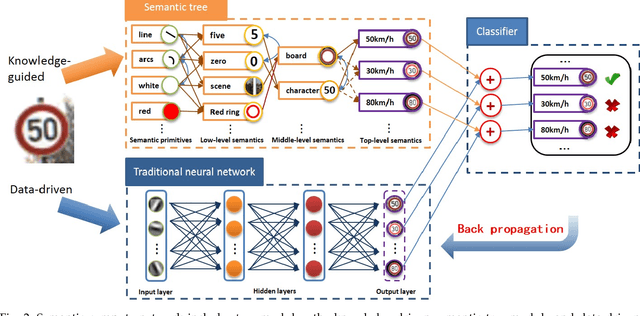
It is very useful to integrate human knowledge and experience into traditional neural networks for faster learning speed, fewer training samples and better interpretability. However, due to the obscured and indescribable black box model of neural networks, it is very difficult to design its architecture, interpret its features and predict its performance. Inspired by human visual cognition process, we propose a knowledge-guided semantic computing network which includes two modules: a knowledge-guided semantic tree and a data-driven neural network. The semantic tree is pre-defined to describe the spatial structural relations of different semantics, which just corresponds to the tree-like description of objects based on human knowledge. The object recognition process through the semantic tree only needs simple forward computing without training. Besides, to enhance the recognition ability of the semantic tree in aspects of the diversity, randomicity and variability, we use the traditional neural network to aid the semantic tree to learn some indescribable features. Only in this case, the training process is needed. The experimental results on MNIST and GTSRB datasets show that compared with the traditional data-driven network, our proposed semantic computing network can achieve better performance with fewer training samples and lower computational complexity. Especially, Our model also has better adversarial robustness than traditional neural network with the help of human knowledge.