Implicit neural representation of textures

Implicit neural representation (INR) has proven to be accurate and efficient in various domains. In this work, we explore how different neural networks can be designed as a new texture INR, which operates in a continuous manner rather than a discrete one over the input UV coordinate space. Through thorough experiments, we demonstrate that these INRs perform well in terms of image quality, with considerable memory usage and rendering inference time. We analyze the balance between these objectives. In addition, we investigate various related applications in real-time rendering and down-stream tasks, e.g. mipmap fitting and INR-space generation.

Machine Learning for Energy-Performance-aware Scheduling

In the post-Dennard era, optimizing embedded systems requires navigating complex trade-offs between energy efficiency and latency. Traditional heuristic tuning is often inefficient in such high-dimensional, non-smooth landscapes. In this work, we propose a Bayesian Optimization framework using Gaussian Processes to automate the search for optimal scheduling configurations on heterogeneous multi-core architectures. We explicitly address the multi-objective nature of the problem by approximating the Pareto Frontier between energy and time. Furthermore, by incorporating Sensitivity Analysis (fANOVA) and comparing different covariance kernels (e.g., Matérn vs. RBF), we provide physical interpretability to the black-box model, revealing the dominant hardware parameters driving system performance.

MeanFlow Transformers with Representation Autoencoders

MeanFlow (MF) is a diffusion-motivated generative model that enables efficient few-step generation by learning long jumps directly from noise to data. In practice, it is often used as a latent MF by leveraging the pre-trained Stable Diffusion variational autoencoder (SD-VAE) for high-dimensional data modeling. However, MF training remains computationally demanding and is often unstable. During inference, the SD-VAE decoder dominates the generation cost, and MF depends on complex guidance hyperparameters for class-conditional generation. In this work, we develop an efficient training and sampling scheme for MF in the latent space of a Representation Autoencoder (RAE), where a pre-trained vision encoder (e.g., DINO) provides semantically rich latents paired with a lightweight decoder. We observe that naive MF training in the RAE latent space suffers from severe gradient explosion. To stabilize and accelerate training, we adopt Consistency Mid-Training for trajectory-aware initialization and use a two-stage scheme: distillation from a pre-trained flow matching teacher to speed convergence and reduce variance, followed by an optional bootstrapping stage with a one-point velocity estimator to further reduce deviation from the oracle mean flow. This design removes the need for guidance, simplifies training configurations, and reduces computation in both training and sampling. Empirically, our method achieves a 1-step FID of 2.03, outperforming vanilla MF's 3.43, while reducing sampling GFLOPS by 38% and total training cost by 83% on ImageNet 256. We further scale our approach to ImageNet 512, achieving a competitive 1-step FID of 3.23 with the lowest GFLOPS among all baselines. Code is available at https://github.com/sony/mf-rae.

RaC: Robot Learning for Long-Horizon Tasks by Scaling Recovery and Correction

Modern paradigms for robot imitation train expressive policy architectures on large amounts of human demonstration data. Yet performance on contact-rich, deformable-object, and long-horizon tasks plateau far below perfect execution, even with thousands of expert demonstrations. This is due to the inefficiency of existing ``expert'' data collection procedures based on human teleoperation. To address this issue, we introduce RaC, a new phase of training on human-in-the-loop rollouts after imitation learning pre-training. In RaC, we fine-tune a robotic policy on human intervention trajectories that illustrate recovery and correction behaviors. Specifically, during a policy rollout, human operators intervene when failure appears imminent, first rewinding the robot back to a familiar, in-distribution state and then providing a corrective segment that completes the current sub-task. Training on this data composition expands the robotic skill repertoire to include retry and adaptation behaviors, which we show are crucial for boosting both efficiency and robustness on long-horizon tasks. Across three real-world bimanual control tasks: shirt hanging, airtight container lid sealing, takeout box packing, and a simulated assembly task, RaC outperforms the prior state-of-the-art using 10$\times$ less data collection time and samples. We also show that RaC enables test-time scaling: the performance of the trained RaC policy scales linearly in the number of recovery maneuvers it exhibits. Videos of the learned policy are available at https://rac-scaling-robot.github.io/.

CHOrD: Generation of Collision-Free, House-Scale, and Organized Digital Twins for 3D Indoor Scenes with Controllable Floor Plans and Optimal Layouts

We introduce CHOrD, a novel framework for scalable synthesis of 3D indoor scenes, designed to create house-scale, collision-free, and hierarchically structured indoor digital twins. In contrast to existing methods that directly synthesize the scene layout as a scene graph or object list, CHOrD incorporates a 2D image-based intermediate layout representation, enabling effective prevention of collision artifacts by successfully capturing them as out-of-distribution (OOD) scenarios during generation. Furthermore, unlike existing methods, CHOrD is capable of generating scene layouts that adhere to complex floor plans with multi-modal controls, enabling the creation of coherent, house-wide layouts robust to both geometric and semantic variations in room structures. Additionally, we propose a novel dataset with expanded coverage of household items and room configurations, as well as significantly improved data quality. CHOrD demonstrates state-of-the-art performance on both the 3D-FRONT and our proposed datasets, delivering photorealistic, spatially coherent indoor scene synthesis adaptable to arbitrary floor plan variations.

Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators

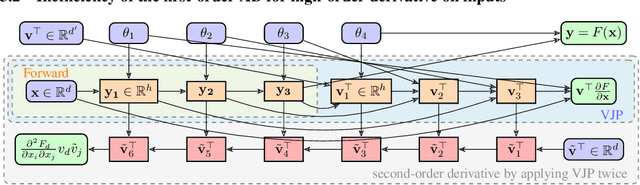
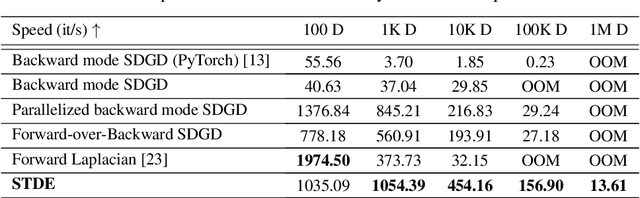
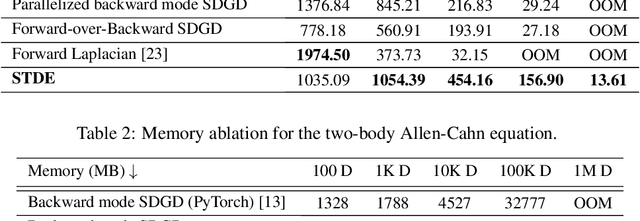
Optimizing neural networks with loss that contain high-dimensional and high-order differential operators is expensive to evaluate with back-propagation due to $\mathcal{O}(d^{k})$ scaling of the derivative tensor size and the $\mathcal{O}(2^{k-1}L)$ scaling in the computation graph, where $d$ is the dimension of the domain, $L$ is the number of ops in the forward computation graph, and $k$ is the derivative order. In previous works, the polynomial scaling in $d$ was addressed by amortizing the computation over the optimization process via randomization. Separately, the exponential scaling in $k$ for univariate functions ($d=1$) was addressed with high-order auto-differentiation (AD). In this work, we show how to efficiently perform arbitrary contraction of the derivative tensor of arbitrary order for multivariate functions, by properly constructing the input tangents to univariate high-order AD, which can be used to efficiently randomize any differential operator. When applied to Physics-Informed Neural Networks (PINNs), our method provides >1000$\times$ speed-up and >30$\times$ memory reduction over randomization with first-order AD, and we can now solve \emph{1-million-dimensional PDEs in 8 minutes on a single NVIDIA A100 GPU}. This work opens the possibility of using high-order differential operators in large-scale problems.

State-space models are accurate and efficient neural operators for dynamical systems

Physics-informed machine learning (PIML) has emerged as a promising alternative to classical methods for predicting dynamical systems, offering faster and more generalizable solutions. However, existing models, including recurrent neural networks (RNNs), transformers, and neural operators, face challenges such as long-time integration, long-range dependencies, chaotic dynamics, and extrapolation, to name a few. To this end, this paper introduces state-space models implemented in Mamba for accurate and efficient dynamical system operator learning. Mamba addresses the limitations of existing architectures by dynamically capturing long-range dependencies and enhancing computational efficiency through reparameterization techniques. To extensively test Mamba and compare against another 11 baselines, we introduce several strict extrapolation testbeds that go beyond the standard interpolation benchmarks. We demonstrate Mamba's superior performance in both interpolation and challenging extrapolation tasks. Mamba consistently ranks among the top models while maintaining the lowest computational cost and exceptional extrapolation capabilities. Moreover, we demonstrate the good performance of Mamba for a real-world application in quantitative systems pharmacology for assessing the efficacy of drugs in tumor growth under limited data scenarios. Taken together, our findings highlight Mamba's potential as a powerful tool for advancing scientific machine learning in dynamical systems modeling. (The code will be available at https://github.com/zheyuanhu01/State_Space_Model_Neural_Operator upon acceptance.)

Tackling the Curse of Dimensionality in Fractional and Tempered Fractional PDEs with Physics-Informed Neural Networks

Fractional and tempered fractional partial differential equations (PDEs) are effective models of long-range interactions, anomalous diffusion, and non-local effects. Traditional numerical methods for these problems are mesh-based, thus struggling with the curse of dimensionality (CoD). Physics-informed neural networks (PINNs) offer a promising solution due to their universal approximation, generalization ability, and mesh-free training. In principle, Monte Carlo fractional PINN (MC-fPINN) estimates fractional derivatives using Monte Carlo methods and thus could lift CoD. However, this may cause significant variance and errors, hence affecting convergence; in addition, MC-fPINN is sensitive to hyperparameters. In general, numerical methods and specifically PINNs for tempered fractional PDEs are under-developed. Herein, we extend MC-fPINN to tempered fractional PDEs to address these issues, resulting in the Monte Carlo tempered fractional PINN (MC-tfPINN). To reduce possible high variance and errors from Monte Carlo sampling, we replace the one-dimensional (1D) Monte Carlo with 1D Gaussian quadrature, applicable to both MC-fPINN and MC-tfPINN. We validate our methods on various forward and inverse problems of fractional and tempered fractional PDEs, scaling up to 100,000 dimensions. Our improved MC-fPINN/MC-tfPINN using quadrature consistently outperforms the original versions in accuracy and convergence speed in very high dimensions.

Score-fPINN: Fractional Score-Based Physics-Informed Neural Networks for High-Dimensional Fokker-Planck-Levy Equations

We introduce an innovative approach for solving high-dimensional Fokker-Planck-L\'evy (FPL) equations in modeling non-Brownian processes across disciplines such as physics, finance, and ecology. We utilize a fractional score function and Physical-informed neural networks (PINN) to lift the curse of dimensionality (CoD) and alleviate numerical overflow from exponentially decaying solutions with dimensions. The introduction of a fractional score function allows us to transform the FPL equation into a second-order partial differential equation without fractional Laplacian and thus can be readily solved with standard physics-informed neural networks (PINNs). We propose two methods to obtain a fractional score function: fractional score matching (FSM) and score-fPINN for fitting the fractional score function. While FSM is more cost-effective, it relies on known conditional distributions. On the other hand, score-fPINN is independent of specific stochastic differential equations (SDEs) but requires evaluating the PINN model's derivatives, which may be more costly. We conduct our experiments on various SDEs and demonstrate numerical stability and effectiveness of our method in dealing with high-dimensional problems, marking a significant advancement in addressing the CoD in FPL equations.

Yell At Your Robot: Improving On-the-Fly from Language Corrections

Hierarchical policies that combine language and low-level control have been shown to perform impressively long-horizon robotic tasks, by leveraging either zero-shot high-level planners like pretrained language and vision-language models (LLMs/VLMs) or models trained on annotated robotic demonstrations. However, for complex and dexterous skills, attaining high success rates on long-horizon tasks still represents a major challenge -- the longer the task is, the more likely it is that some stage will fail. Can humans help the robot to continuously improve its long-horizon task performance through intuitive and natural feedback? In this paper, we make the following observation: high-level policies that index into sufficiently rich and expressive low-level language-conditioned skills can be readily supervised with human feedback in the form of language corrections. We show that even fine-grained corrections, such as small movements ("move a bit to the left"), can be effectively incorporated into high-level policies, and that such corrections can be readily obtained from humans observing the robot and making occasional suggestions. This framework enables robots not only to rapidly adapt to real-time language feedback, but also incorporate this feedback into an iterative training scheme that improves the high-level policy's ability to correct errors in both low-level execution and high-level decision-making purely from verbal feedback. Our evaluation on real hardware shows that this leads to significant performance improvement in long-horizon, dexterous manipulation tasks without the need for any additional teleoperation. Videos and code are available at https://yay-robot.github.io/.