An Empirical Study of Federated Prompt Learning for Vision Language Model

The Vision Language Model (VLM) excels in aligning vision and language representations, and prompt learning has emerged as a key technique for adapting such models to downstream tasks. However, the application of prompt learning with VLM in federated learning (\fl{}) scenarios remains underexplored. This paper systematically investigates the behavioral differences between language prompt learning (LPT) and vision prompt learning (VPT) under data heterogeneity challenges, including label skew and domain shift. We conduct extensive experiments to evaluate the impact of various \fl{} and prompt configurations, such as client scale, aggregation strategies, and prompt length, to assess the robustness of Federated Prompt Learning (FPL). Furthermore, we explore strategies for enhancing prompt learning in complex scenarios where label skew and domain shift coexist, including leveraging both prompt types when computational resources allow. Our findings offer practical insights into optimizing prompt learning in federated settings, contributing to the broader deployment of VLMs in privacy-preserving environments.

Keeping Yourself is Important in Downstream Tuning Multimodal Large Language Model

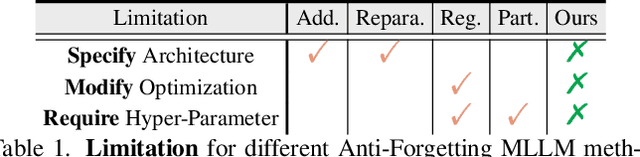
Multi-modal Large Language Models (MLLMs) integrate visual and linguistic reasoning to address complex tasks such as image captioning and visual question answering. While MLLMs demonstrate remarkable versatility, MLLMs appears limited performance on special applications. But tuning MLLMs for downstream tasks encounters two key challenges: Task-Expert Specialization, where distribution shifts between pre-training and target datasets constrain target performance, and Open-World Stabilization, where catastrophic forgetting erases the model general knowledge. In this work, we systematically review recent advancements in MLLM tuning methodologies, classifying them into three paradigms: (I) Selective Tuning, (II) Additive Tuning, and (III) Reparameterization Tuning. Furthermore, we benchmark these tuning strategies across popular MLLM architectures and diverse downstream tasks to establish standardized evaluation analysis and systematic tuning principles. Finally, we highlight several open challenges in this domain and propose future research directions. To facilitate ongoing progress in this rapidly evolving field, we provide a public repository that continuously tracks developments: https://github.com/WenkeHuang/Awesome-MLLM-Tuning.

Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators

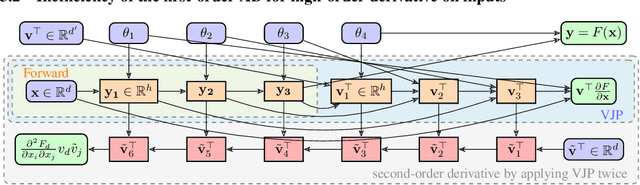
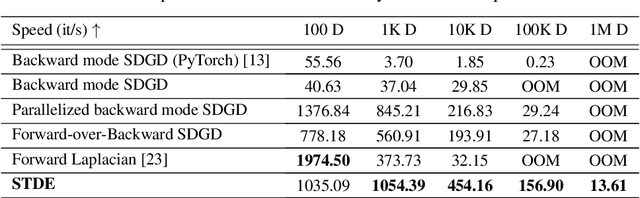
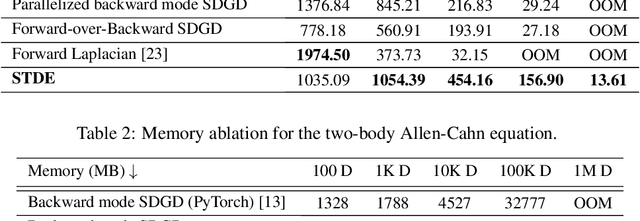
Optimizing neural networks with loss that contain high-dimensional and high-order differential operators is expensive to evaluate with back-propagation due to $\mathcal{O}(d^{k})$ scaling of the derivative tensor size and the $\mathcal{O}(2^{k-1}L)$ scaling in the computation graph, where $d$ is the dimension of the domain, $L$ is the number of ops in the forward computation graph, and $k$ is the derivative order. In previous works, the polynomial scaling in $d$ was addressed by amortizing the computation over the optimization process via randomization. Separately, the exponential scaling in $k$ for univariate functions ($d=1$) was addressed with high-order auto-differentiation (AD). In this work, we show how to efficiently perform arbitrary contraction of the derivative tensor of arbitrary order for multivariate functions, by properly constructing the input tangents to univariate high-order AD, which can be used to efficiently randomize any differential operator. When applied to Physics-Informed Neural Networks (PINNs), our method provides >1000$\times$ speed-up and >30$\times$ memory reduction over randomization with first-order AD, and we can now solve \emph{1-million-dimensional PDEs in 8 minutes on a single NVIDIA A100 GPU}. This work opens the possibility of using high-order differential operators in large-scale problems.

Learn from Downstream and Be Yourself in Multimodal Large Language Model Fine-Tuning

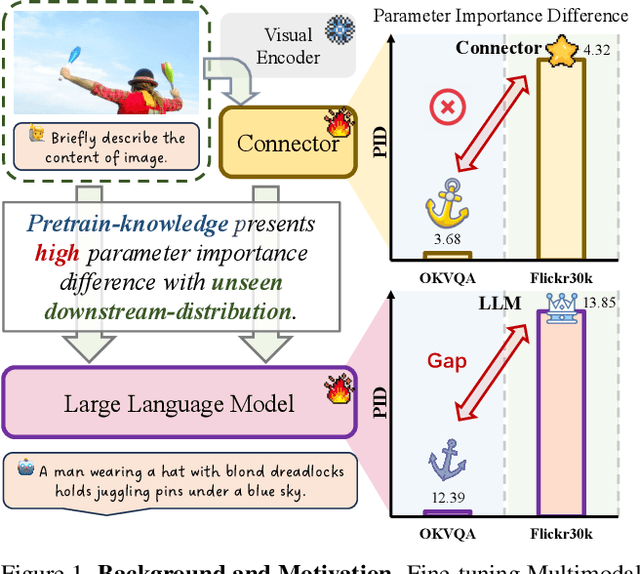
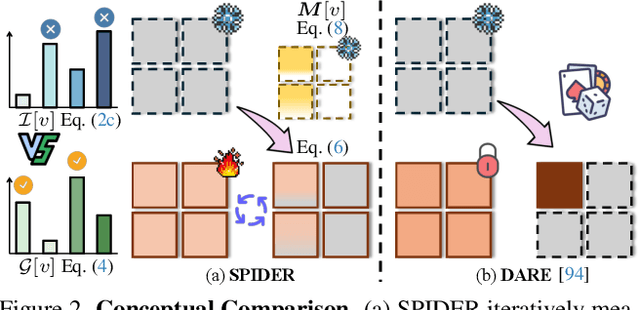
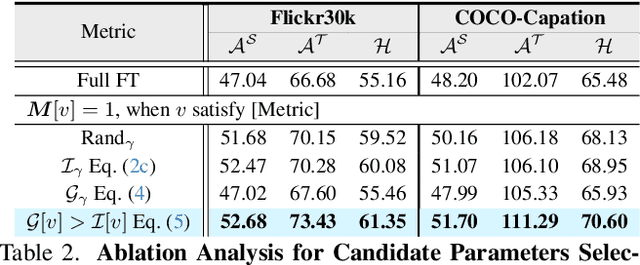
Multimodal Large Language Model (MLLM) have demonstrated strong generalization capabilities across diverse distributions and tasks, largely due to extensive pre-training datasets. Fine-tuning MLLM has become a common practice to improve performance on specific downstream tasks. However, during fine-tuning, MLLM often faces the risk of forgetting knowledge acquired during pre-training, which can result in a decline in generalization abilities. To balance the trade-off between generalization and specialization, we propose measuring the parameter importance for both pre-trained and fine-tuning distributions, based on frozen pre-trained weight magnitude and accumulated fine-tuning gradient values. We further apply an importance-aware weight allocation strategy, selectively updating relatively important parameters for downstream tasks. We conduct empirical evaluations on both image captioning and visual question-answering tasks using various MLLM architectures. The comprehensive experimental analysis demonstrates the effectiveness of the proposed solution, highlighting the efficiency of the crucial modules in enhancing downstream specialization performance while mitigating generalization degradation in MLLM Fine-Tuning.

Diagonalization without Diagonalization: A Direct Optimization Approach for Solid-State Density Functional Theory

We present a novel approach to address the challenges of variable occupation numbers in direct optimization of density functional theory (DFT). By parameterizing both the eigenfunctions and the occupation matrix, our method minimizes the free energy with respect to these parameters. As the stationary conditions require the occupation matrix and the Kohn-Sham Hamiltonian to be simultaneously diagonalizable, this leads to the concept of ``self-diagonalization,'' where, by assuming a diagonal occupation matrix without loss of generality, the Hamiltonian matrix naturally becomes diagonal at stationary points. Our method incorporates physical constraints on both the eigenfunctions and the occupations into the parameterization, transforming the constrained optimization into an fully differentiable unconstrained problem, which is solvable via gradient descent. Implemented in JAX, our method was tested on aluminum and silicon, confirming that it achieves efficient self-diagonalization, produces the correct Fermi-Dirac distribution of the occupation numbers and yields band structures consistent with those obtained with SCF methods in Quantum Espresso.

Hutchinson Trace Estimation for High-Dimensional and High-Order Physics-Informed Neural Networks

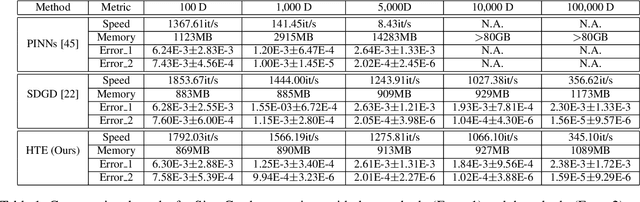
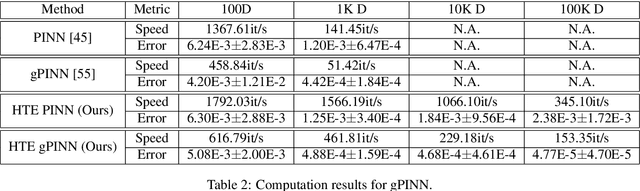
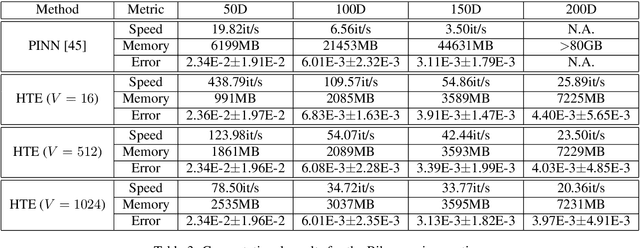
Physics-Informed Neural Networks (PINNs) have proven effective in solving partial differential equations (PDEs), especially when some data are available by blending seamlessly data and physics. However, extending PINNs to high-dimensional and even high-order PDEs encounters significant challenges due to the computational cost associated with automatic differentiation in the residual loss. Herein, we address the limitations of PINNs in handling high-dimensional and high-order PDEs by introducing Hutchinson Trace Estimation (HTE). Starting with the second-order high-dimensional PDEs ubiquitous in scientific computing, HTE transforms the calculation of the entire Hessian matrix into a Hessian vector product (HVP). This approach alleviates the computational bottleneck via Taylor-mode automatic differentiation and significantly reduces memory consumption from the Hessian matrix to HVP. We further showcase HTE's convergence to the original PINN loss and its unbiased behavior under specific conditions. Comparisons with Stochastic Dimension Gradient Descent (SDGD) highlight the distinct advantages of HTE, particularly in scenarios with significant variance among dimensions. We further extend HTE to higher-order and higher-dimensional PDEs, specifically addressing the biharmonic equation. By employing tensor-vector products (TVP), HTE efficiently computes the colossal tensor associated with the fourth-order high-dimensional biharmonic equation, saving memory and enabling rapid computation. The effectiveness of HTE is illustrated through experimental setups, demonstrating comparable convergence rates with SDGD under memory and speed constraints. Additionally, HTE proves valuable in accelerating the Gradient-Enhanced PINN (gPINN) version as well as the Biharmonic equation. Overall, HTE opens up a new capability in scientific machine learning for tackling high-order and high-dimensional PDEs.

Federated Learning for Generalization, Robustness, Fairness: A Survey and Benchmark

Federated learning has emerged as a promising paradigm for privacy-preserving collaboration among different parties. Recently, with the popularity of federated learning, an influx of approaches have delivered towards different realistic challenges. In this survey, we provide a systematic overview of the important and recent developments of research on federated learning. Firstly, we introduce the study history and terminology definition of this area. Then, we comprehensively review three basic lines of research: generalization, robustness, and fairness, by introducing their respective background concepts, task settings, and main challenges. We also offer a detailed overview of representative literature on both methods and datasets. We further benchmark the reviewed methods on several well-known datasets. Finally, we point out several open issues in this field and suggest opportunities for further research. We also provide a public website to continuously track developments in this fast advancing field: https://github.com/WenkeHuang/MarsFL.

Generalizable Heterogeneous Federated Cross-Correlation and Instance Similarity Learning

Federated learning is an important privacy-preserving multi-party learning paradigm, involving collaborative learning with others and local updating on private data. Model heterogeneity and catastrophic forgetting are two crucial challenges, which greatly limit the applicability and generalizability. This paper presents a novel FCCL+, federated correlation and similarity learning with non-target distillation, facilitating the both intra-domain discriminability and inter-domain generalization. For heterogeneity issue, we leverage irrelevant unlabeled public data for communication between the heterogeneous participants. We construct cross-correlation matrix and align instance similarity distribution on both logits and feature levels, which effectively overcomes the communication barrier and improves the generalizable ability. For catastrophic forgetting in local updating stage, FCCL+ introduces Federated Non Target Distillation, which retains inter-domain knowledge while avoiding the optimization conflict issue, fulling distilling privileged inter-domain information through depicting posterior classes relation. Considering that there is no standard benchmark for evaluating existing heterogeneous federated learning under the same setting, we present a comprehensive benchmark with extensive representative methods under four domain shift scenarios, supporting both heterogeneous and homogeneous federated settings. Empirical results demonstrate the superiority of our method and the efficiency of modules on various scenarios.

Model-based Deep Reinforcement Learning for Dynamic Portfolio Optimization

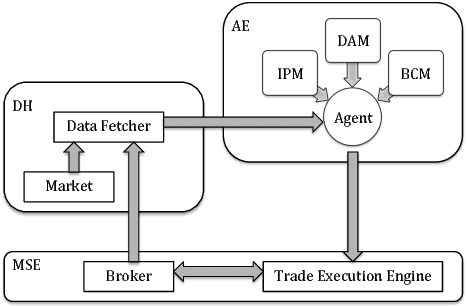
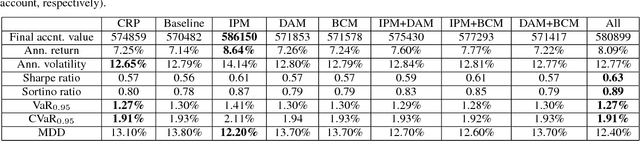
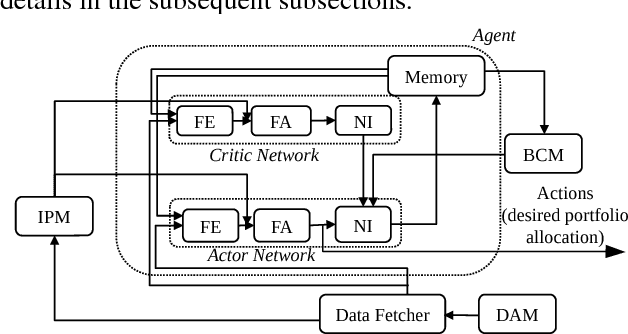
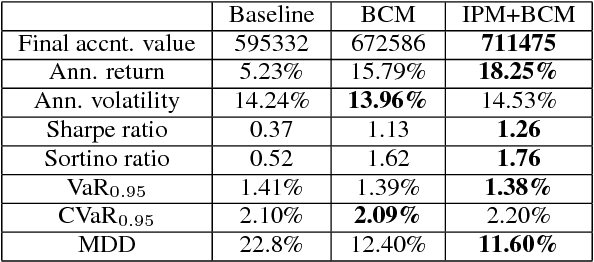
Dynamic portfolio optimization is the process of sequentially allocating wealth to a collection of assets in some consecutive trading periods, based on investors' return-risk profile. Automating this process with machine learning remains a challenging problem. Here, we design a deep reinforcement learning (RL) architecture with an autonomous trading agent such that, investment decisions and actions are made periodically, based on a global objective, with autonomy. In particular, without relying on a purely model-free RL agent, we train our trading agent using a novel RL architecture consisting of an infused prediction module (IPM), a generative adversarial data augmentation module (DAM) and a behavior cloning module (BCM). Our model-based approach works with both on-policy or off-policy RL algorithms. We further design the back-testing and execution engine which interact with the RL agent in real time. Using historical {\em real} financial market data, we simulate trading with practical constraints, and demonstrate that our proposed model is robust, profitable and risk-sensitive, as compared to baseline trading strategies and model-free RL agents from prior work.