Hutchinson Trace Estimation for High-Dimensional and High-Order Physics-Informed Neural Networks
Paper and Code
Dec 22, 2023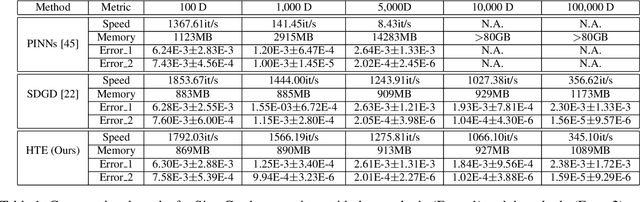
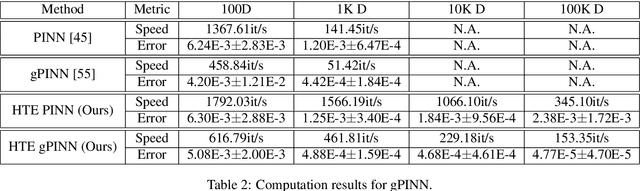
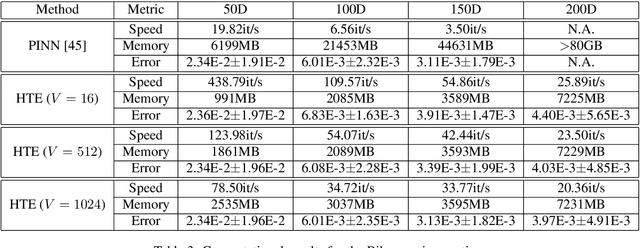
Physics-Informed Neural Networks (PINNs) have proven effective in solving partial differential equations (PDEs), especially when some data are available by blending seamlessly data and physics. However, extending PINNs to high-dimensional and even high-order PDEs encounters significant challenges due to the computational cost associated with automatic differentiation in the residual loss. Herein, we address the limitations of PINNs in handling high-dimensional and high-order PDEs by introducing Hutchinson Trace Estimation (HTE). Starting with the second-order high-dimensional PDEs ubiquitous in scientific computing, HTE transforms the calculation of the entire Hessian matrix into a Hessian vector product (HVP). This approach alleviates the computational bottleneck via Taylor-mode automatic differentiation and significantly reduces memory consumption from the Hessian matrix to HVP. We further showcase HTE's convergence to the original PINN loss and its unbiased behavior under specific conditions. Comparisons with Stochastic Dimension Gradient Descent (SDGD) highlight the distinct advantages of HTE, particularly in scenarios with significant variance among dimensions. We further extend HTE to higher-order and higher-dimensional PDEs, specifically addressing the biharmonic equation. By employing tensor-vector products (TVP), HTE efficiently computes the colossal tensor associated with the fourth-order high-dimensional biharmonic equation, saving memory and enabling rapid computation. The effectiveness of HTE is illustrated through experimental setups, demonstrating comparable convergence rates with SDGD under memory and speed constraints. Additionally, HTE proves valuable in accelerating the Gradient-Enhanced PINN (gPINN) version as well as the Biharmonic equation. Overall, HTE opens up a new capability in scientific machine learning for tackling high-order and high-dimensional PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge