Memory-Efficient Gradient Unrolling for Large-Scale Bi-level Optimization

Bi-level optimization (BO) has become a fundamental mathematical framework for addressing hierarchical machine learning problems. As deep learning models continue to grow in size, the demand for scalable bi-level optimization solutions has become increasingly critical. Traditional gradient-based bi-level optimization algorithms, due to their inherent characteristics, are ill-suited to meet the demands of large-scale applications. In this paper, we introduce $\textbf{F}$orward $\textbf{G}$radient $\textbf{U}$nrolling with $\textbf{F}$orward $\textbf{F}$radient, abbreviated as $(\textbf{FG})^2\textbf{U}$, which achieves an unbiased stochastic approximation of the meta gradient for bi-level optimization. $(\text{FG})^2\text{U}$ circumvents the memory and approximation issues associated with classical bi-level optimization approaches, and delivers significantly more accurate gradient estimates than existing large-scale bi-level optimization approaches. Additionally, $(\text{FG})^2\text{U}$ is inherently designed to support parallel computing, enabling it to effectively leverage large-scale distributed computing systems to achieve significant computational efficiency. In practice, $(\text{FG})^2\text{U}$ and other methods can be strategically placed at different stages of the training process to achieve a more cost-effective two-phase paradigm. Further, $(\text{FG})^2\text{U}$ is easy to implement within popular deep learning frameworks, and can be conveniently adapted to address more challenging zeroth-order bi-level optimization scenarios. We provide a thorough convergence analysis and a comprehensive practical discussion for $(\text{FG})^2\text{U}$, complemented by extensive empirical evaluations, showcasing its superior performance in diverse large-scale bi-level optimization tasks.

Understanding Training-free Diffusion Guidance: Mechanisms and Limitations

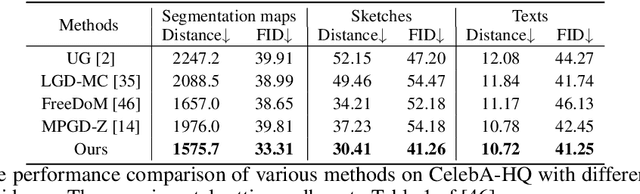
Adding additional control to pretrained diffusion models has become an increasingly popular research area, with extensive applications in computer vision, reinforcement learning, and AI for science. Recently, several studies have proposed training-free diffusion guidance by using off-the-shelf networks pretrained on clean images. This approach enables zero-shot conditional generation for universal control formats, which appears to offer a free lunch in diffusion guidance. In this paper, we aim to develop a deeper understanding of the operational mechanisms and fundamental limitations of training-free guidance. We offer a theoretical analysis that supports training-free guidance from the perspective of optimization, distinguishing it from classifier-based (or classifier-free) guidance. To elucidate their drawbacks, we theoretically demonstrate that training-free methods are more susceptible to adversarial gradients and exhibit slower convergence rates compared to classifier guidance. We then introduce a collection of techniques designed to overcome the limitations, accompanied by theoretical rationale and empirical evidence. Our experiments in image and motion generation confirm the efficacy of these techniques.

Bias-Variance Trade-off in Physics-Informed Neural Networks with Randomized Smoothing for High-Dimensional PDEs

While physics-informed neural networks (PINNs) have been proven effective for low-dimensional partial differential equations (PDEs), the computational cost remains a hurdle in high-dimensional scenarios. This is particularly pronounced when computing high-order and high-dimensional derivatives in the physics-informed loss. Randomized Smoothing PINN (RS-PINN) introduces Gaussian noise for stochastic smoothing of the original neural net model, enabling Monte Carlo methods for derivative approximation, eliminating the need for costly auto-differentiation. Despite its computational efficiency in high dimensions, RS-PINN introduces biases in both loss and gradients, negatively impacting convergence, especially when coupled with stochastic gradient descent (SGD). We present a comprehensive analysis of biases in RS-PINN, attributing them to the nonlinearity of the Mean Squared Error (MSE) loss and the PDE nonlinearity. We propose tailored bias correction techniques based on the order of PDE nonlinearity. The unbiased RS-PINN allows for a detailed examination of its pros and cons compared to the biased version. Specifically, the biased version has a lower variance and runs faster than the unbiased version, but it is less accurate due to the bias. To optimize the bias-variance trade-off, we combine the two approaches in a hybrid method that balances the rapid convergence of the biased version with the high accuracy of the unbiased version. In addition, we present an enhanced implementation of RS-PINN. Extensive experiments on diverse high-dimensional PDEs, including Fokker-Planck, HJB, viscous Burgers', Allen-Cahn, and Sine-Gordon equations, illustrate the bias-variance trade-off and highlight the effectiveness of the hybrid RS-PINN. Empirical guidelines are provided for selecting biased, unbiased, or hybrid versions, depending on the dimensionality and nonlinearity of the specific PDE problem.

SPE: Symmetrical Prompt Enhancement for Fact Probing

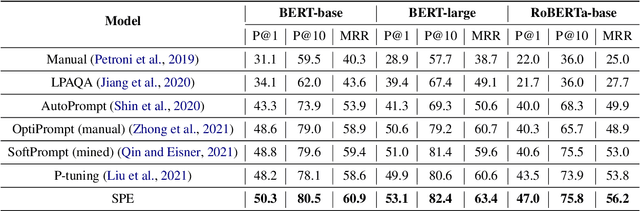
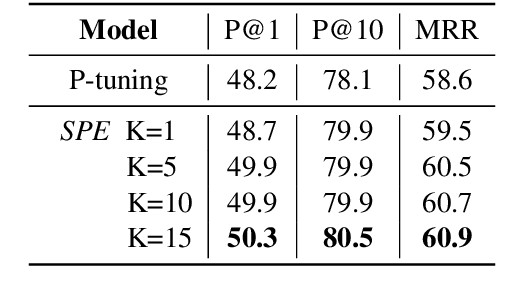
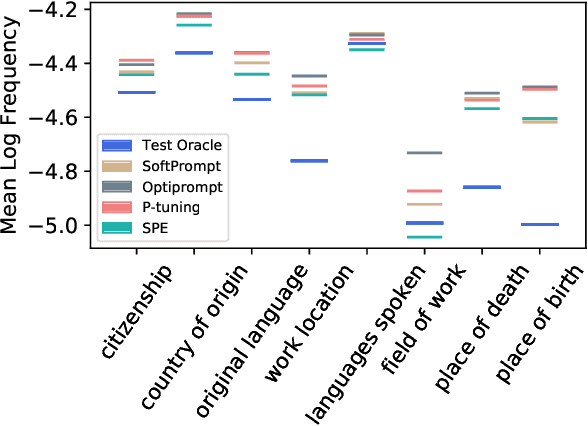
Pretrained language models (PLMs) have been shown to accumulate factual knowledge during pretrainingng (Petroni et al., 2019). Recent works probe PLMs for the extent of this knowledge through prompts either in discrete or continuous forms. However, these methods do not consider symmetry of the task: object prediction and subject prediction. In this work, we propose Symmetrical Prompt Enhancement (SPE), a continuous prompt-based method for factual probing in PLMs that leverages the symmetry of the task by constructing symmetrical prompts for subject and object prediction. Our results on a popular factual probing dataset, LAMA, show significant improvement of SPE over previous probing methods.

Your Autoregressive Generative Model Can be Better If You Treat It as an Energy-Based One

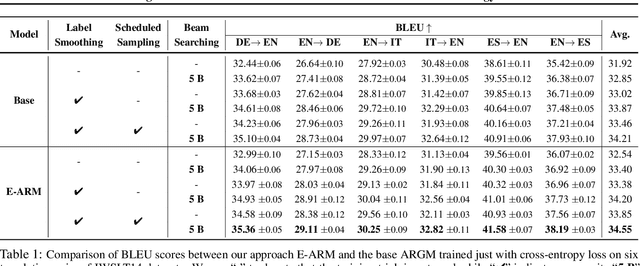
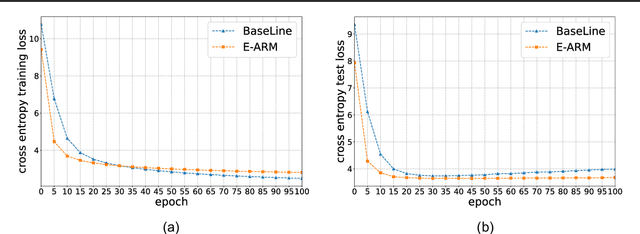
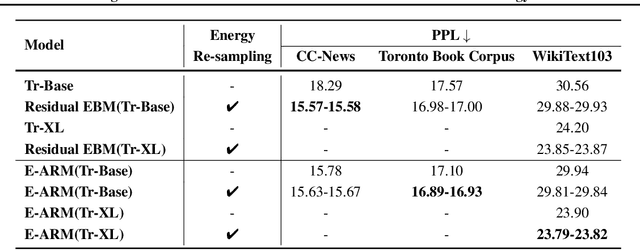
Autoregressive generative models are commonly used, especially for those tasks involving sequential data. They have, however, been plagued by a slew of inherent flaws due to the intrinsic characteristics of chain-style conditional modeling (e.g., exposure bias or lack of long-range coherence), severely limiting their ability to model distributions properly. In this paper, we propose a unique method termed E-ARM for training autoregressive generative models that takes advantage of a well-designed energy-based learning objective. By leveraging the extra degree of freedom of the softmax operation, we are allowed to make the autoregressive model itself be an energy-based model for measuring the likelihood of input without introducing any extra parameters. Furthermore, we show that E-ARM can be trained efficiently and is capable of alleviating the exposure bias problem and increase temporal coherence for autoregressive generative models. Extensive empirical results, covering benchmarks like language modeling, neural machine translation, and image generation, demonstrate the effectiveness of the proposed approach.

Sparse Fusion Mixture-of-Experts are Domain Generalizable Learners

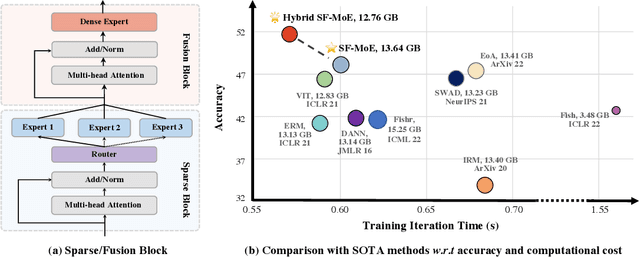
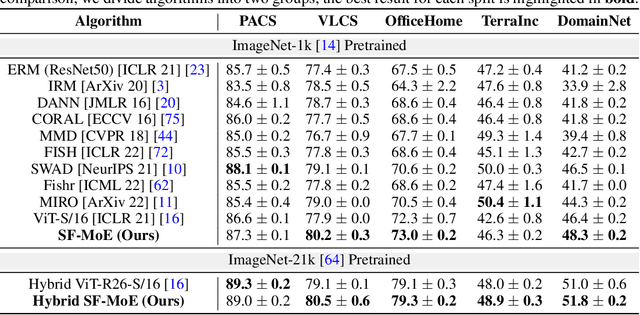
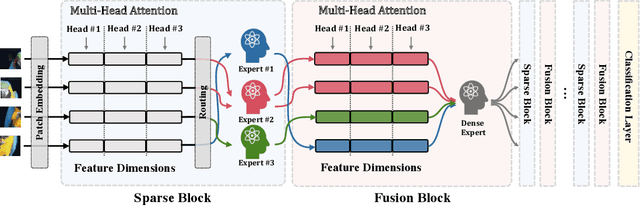
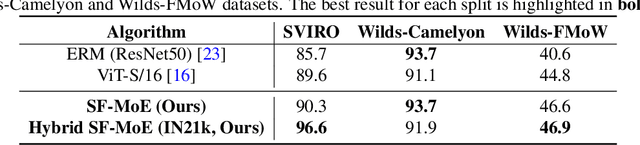
Domain generalization (DG) aims at learning generalizable models under distribution shifts to avoid redundantly overfitting massive training data. Previous works with complex loss design and gradient constraint have not yet led to empirical success on large-scale benchmarks. In this work, we reveal the mixture-of-experts (MoE) model's generalizability on DG by leveraging to distributively handle multiple aspects of the predictive features across domains. To this end, we propose Sparse Fusion Mixture-of-Experts (SF-MoE), which incorporates sparsity and fusion mechanisms into the MoE framework to keep the model both sparse and predictive. SF-MoE has two dedicated modules: 1) sparse block and 2) fusion block, which disentangle and aggregate the diverse learned signals of an object, respectively. Extensive experiments demonstrate that SF-MoE is a domain-generalizable learner on large-scale benchmarks. It outperforms state-of-the-art counterparts by more than 2% across 5 large-scale DG datasets (e.g., DomainNet), with the same or even lower computational costs. We further reveal the internal mechanism of SF-MoE from distributed representation perspective (e.g., visual attributes). We hope this framework could facilitate future research to push generalizable object recognition to the real world. Code and models are released at https://github.com/Luodian/SF-MoE-DG.

Energy-Based Open-World Uncertainty Modeling for Confidence Calibration

Confidence calibration is of great importance to the reliability of decisions made by machine learning systems. However, discriminative classifiers based on deep neural networks are often criticized for producing overconfident predictions that fail to reflect the true correctness likelihood of classification accuracy. We argue that such an inability to model uncertainty is mainly caused by the closed-world nature in softmax: a model trained by the cross-entropy loss will be forced to classify input into one of $K$ pre-defined categories with high probability. To address this problem, we for the first time propose a novel $K$+1-way softmax formulation, which incorporates the modeling of open-world uncertainty as the extra dimension. To unify the learning of the original $K$-way classification task and the extra dimension that models uncertainty, we propose a novel energy-based objective function, and moreover, theoretically prove that optimizing such an objective essentially forces the extra dimension to capture the marginal data distribution. Extensive experiments show that our approach, Energy-based Open-World Softmax (EOW-Softmax), is superior to existing state-of-the-art methods in improving confidence calibration.

Invariant Information Bottleneck for Domain Generalization

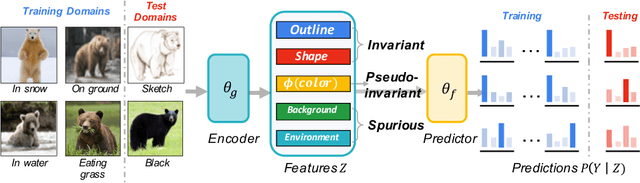
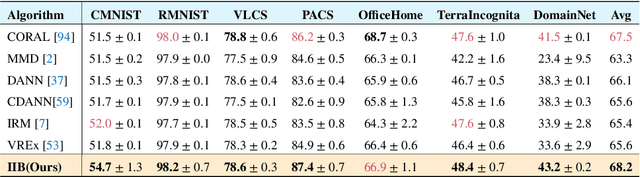
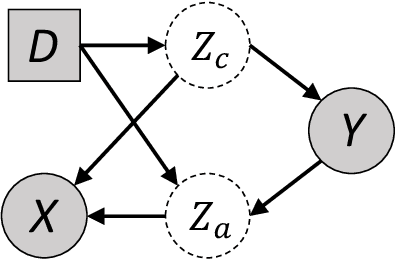
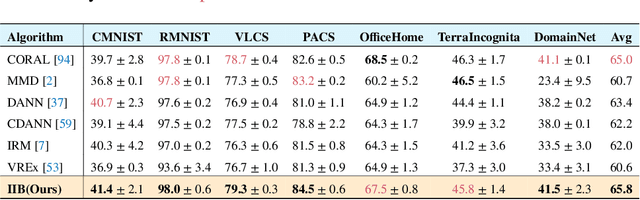
The main challenge for domain generalization (DG) is to overcome the potential distributional shift between multiple training domains and unseen test domains. One popular class of DG algorithms aims to learn representations that have an invariant causal relation across the training domains. However, certain features, called \emph{pseudo-invariant features}, may be invariant in the training domain but not the test domain and can substantially decreases the performance of existing algorithms. To address this issue, we propose a novel algorithm, called Invariant Information Bottleneck (IIB), that learns a minimally sufficient representation that is invariant across training and testing domains. By minimizing the mutual information between the representation and inputs, IIB alleviates its reliance on pseudo-invariant features, which is desirable for DG. To verify the effectiveness of the IIB principle, we conduct extensive experiments on large-scale DG benchmarks. The results show that IIB outperforms invariant learning baseline (e.g. IRM) by an average of 2.8\% and 3.8\% accuracy over two evaluation metrics.

Learning Invariant Representations and Risks for Semi-supervised Domain Adaptation

The success of supervised learning hinges on the assumption that the training and test data come from the same underlying distribution, which is often not valid in practice due to potential distribution shift. In light of this, most existing methods for unsupervised domain adaptation focus on achieving domain-invariant representations and small source domain error. However, recent works have shown that this is not sufficient to guarantee good generalization on the target domain, and in fact, is provably detrimental under label distribution shift. Furthermore, in many real-world applications it is often feasible to obtain a small amount of labeled data from the target domain and use them to facilitate model training with source data. Inspired by the above observations, in this paper we propose the first method that aims to simultaneously learn invariant representations and risks under the setting of semi-supervised domain adaptation (Semi-DA). First, we provide a finite sample bound for both classification and regression problems under Semi-DA. The bound suggests a principled way to obtain target generalization, i.e. by aligning both the marginal and conditional distributions across domains in feature space. Motivated by this, we then introduce the LIRR algorithm for jointly \textbf{L}earning \textbf{I}nvariant \textbf{R}epresentations and \textbf{R}isks. Finally, extensive experiments are conducted on both classification and regression tasks, which demonstrates LIRR consistently achieves state-of-the-art performance and significant improvements compared with the methods that only learn invariant representations or invariant risks.

ePointDA: An End-to-End Simulation-to-Real Domain Adaptation Framework for LiDAR Point Cloud Segmentation

Due to its robust and precise distance measurements, LiDAR plays an important role in scene understanding for autonomous driving. Training deep neural networks (DNNs) on LiDAR data requires large-scale point-wise annotations, which are time-consuming and expensive to obtain. Instead, simulation-to-real domain adaptation (SRDA) trains a DNN using unlimited synthetic data with automatically generated labels and transfers the learned model to real scenarios. Existing SRDA methods for LiDAR point cloud segmentation mainly employ a multi-stage pipeline and focus on feature-level alignment. They require prior knowledge of real-world statistics and ignore the pixel-level dropout noise gap and the spatial feature gap between different domains. In this paper, we propose a novel end-to-end framework, named ePointDA, to address the above issues. Specifically, ePointDA consists of three components: self-supervised dropout noise rendering, statistics-invariant and spatially-adaptive feature alignment, and transferable segmentation learning. The joint optimization enables ePointDA to bridge the domain shift at the pixel-level by explicitly rendering dropout noise for synthetic LiDAR and at the feature-level by spatially aligning the features between different domains, without requiring the real-world statistics. Extensive experiments adapting from synthetic GTA-LiDAR to real KITTI and SemanticKITTI demonstrate the superiority of ePointDA for LiDAR point cloud segmentation.