Invariant Information Bottleneck for Domain Generalization
Paper and Code
Jun 14, 2021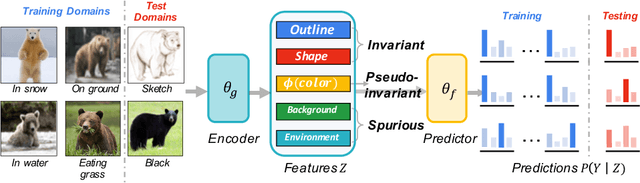
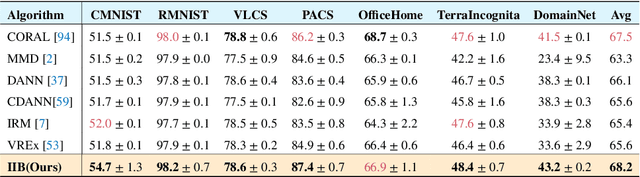
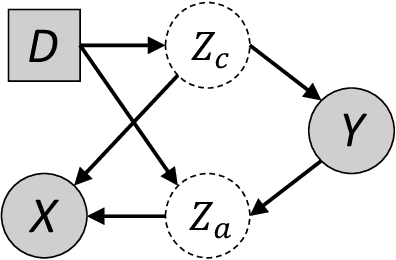
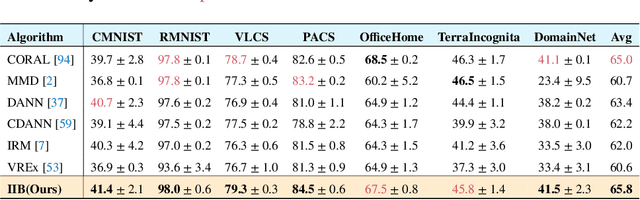
The main challenge for domain generalization (DG) is to overcome the potential distributional shift between multiple training domains and unseen test domains. One popular class of DG algorithms aims to learn representations that have an invariant causal relation across the training domains. However, certain features, called \emph{pseudo-invariant features}, may be invariant in the training domain but not the test domain and can substantially decreases the performance of existing algorithms. To address this issue, we propose a novel algorithm, called Invariant Information Bottleneck (IIB), that learns a minimally sufficient representation that is invariant across training and testing domains. By minimizing the mutual information between the representation and inputs, IIB alleviates its reliance on pseudo-invariant features, which is desirable for DG. To verify the effectiveness of the IIB principle, we conduct extensive experiments on large-scale DG benchmarks. The results show that IIB outperforms invariant learning baseline (e.g. IRM) by an average of 2.8\% and 3.8\% accuracy over two evaluation metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge