Data adaptive RKHS Tikhonov regularization for learning kernels in operators
Paper and Code
Mar 08, 2022
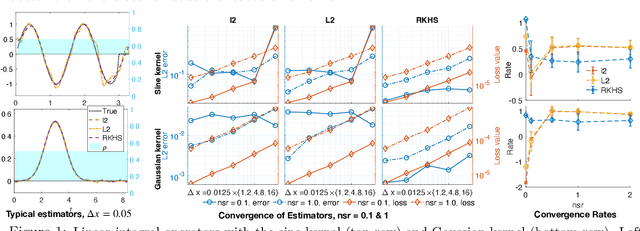
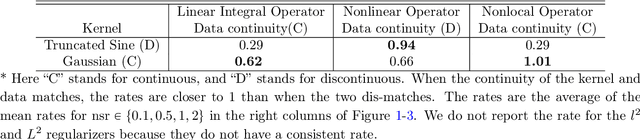
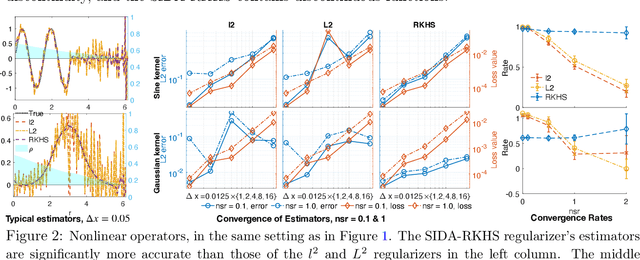
We present DARTR: a Data Adaptive RKHS Tikhonov Regularization method for the linear inverse problem of nonparametric learning of function parameters in operators. A key ingredient is a system intrinsic data-adaptive (SIDA) RKHS, whose norm restricts the learning to take place in the function space of identifiability. DARTR utilizes this norm and selects the regularization parameter by the L-curve method. We illustrate its performance in examples including integral operators, nonlinear operators and nonlocal operators with discrete synthetic data. Numerical results show that DARTR leads to an accurate estimator robust to both numerical error due to discrete data and noise in data, and the estimator converges at a consistent rate as the data mesh refines under different levels of noises, outperforming two baseline regularizers using $l^2$ and $L^2$ norms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge