Nonparametric learning of kernels in nonlocal operators
Paper and Code
May 23, 2022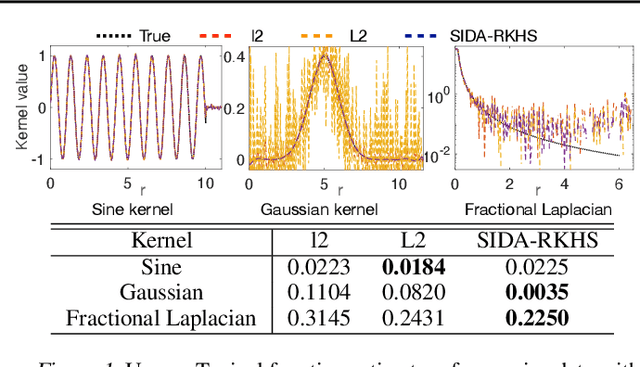
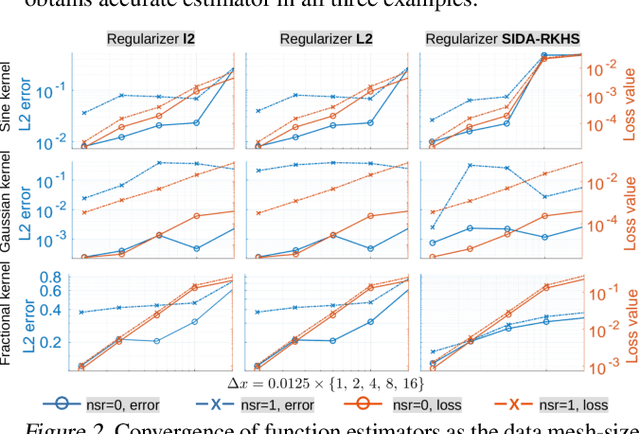
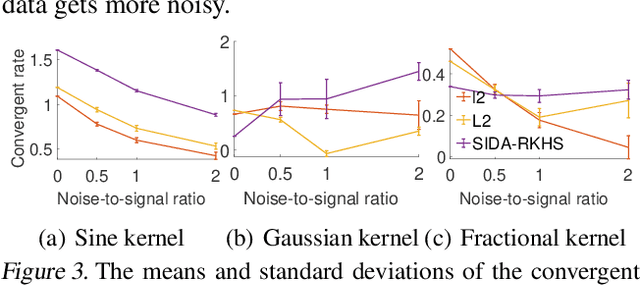
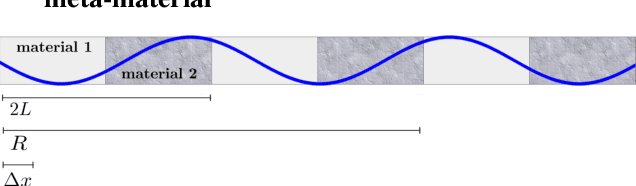
Nonlocal operators with integral kernels have become a popular tool for designing solution maps between function spaces, due to their efficiency in representing long-range dependence and the attractive feature of being resolution-invariant. In this work, we provide a rigorous identifiability analysis and convergence study for the learning of kernels in nonlocal operators. It is found that the kernel learning is an ill-posed or even ill-defined inverse problem, leading to divergent estimators in the presence of modeling errors or measurement noises. To resolve this issue, we propose a nonparametric regression algorithm with a novel data adaptive RKHS Tikhonov regularization method based on the function space of identifiability. The method yields a noisy-robust convergent estimator of the kernel as the data resolution refines, on both synthetic and real-world datasets. In particular, the method successfully learns a homogenized model for the stress wave propagation in a heterogeneous solid, revealing the unknown governing laws from real-world data at microscale. Our regularization method outperforms baseline methods in robustness, generalizability and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge