Graph Fourier Neural Kernels (G-FuNK): Learning Solutions of Nonlinear Diffusive Parametric PDEs on Multiple Domains

Predicting time-dependent dynamics of complex systems governed by non-linear partial differential equations (PDEs) with varying parameters and domains is a challenging task motivated by applications across various fields. We introduce a novel family of neural operators based on our Graph Fourier Neural Kernels, designed to learn solution generators for nonlinear PDEs in which the highest-order term is diffusive, across multiple domains and parameters. G-FuNK combines components that are parameter- and domain-adapted with others that are not. The domain-adapted components are constructed using a weighted graph on the discretized domain, where the graph Laplacian approximates the highest-order diffusive term, ensuring boundary condition compliance and capturing the parameter and domain-specific behavior. Meanwhile, the learned components transfer across domains and parameters via Fourier Neural Operators. This approach naturally embeds geometric and directional information, improving generalization to new test domains without need for retraining the network. To handle temporal dynamics, our method incorporates an integrated ODE solver to predict the evolution of the system. Experiments show G-FuNK's capability to accurately approximate heat, reaction diffusion, and cardiac electrophysiology equations across various geometries and anisotropic diffusivity fields. G-FuNK achieves low relative errors on unseen domains and fiber fields, significantly accelerating predictions compared to traditional finite-element solvers.

Anatomically-Informed Deep Learning on Contrast-Enhanced Cardiac MRI for Scar Segmentation and Clinical Feature Extraction

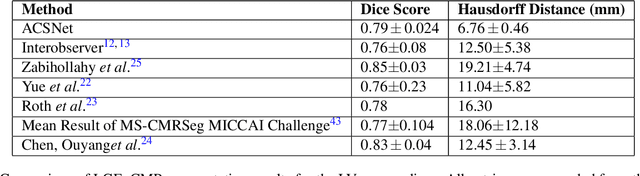
Many cardiac diseases are associated with structural remodeling of the myocardium. Cardiac magnetic resonance (CMR) imaging with contrast enhancement, such as late gadolinium enhancement (LGE), has unparalleled capability to visualize fibrotic tissue remodeling, allowing for direct characterization of the pathophysiological abnormalities leading to arrhythmias and sudden cardiac death (SCD). Automating segmentation of the ventricles with fibrosis distribution could dramatically enhance the utility of LGE-CMR in heart disease clinical research and in the management of patients with risk of arrhythmias and SCD. Here we describe an anatomically-informed deep learning (DL) approach to myocardium and scar segmentation and clinical feature extraction from LGE-CMR images. The technology enables clinical use by ensuring anatomical accuracy and complete automation. Algorithm performance is strong for both myocardium segmentation ($98\%$ accuracy and $0.79$ Dice score in a hold-out test set) and evaluation measures shown to correlate with heart disease, such as scar amount ($6.3\%$ relative error). Our approach for clinical feature extraction, which satisfies highly complex geometric constraints without stunting the learning process, has the potential of a broad applicability in computer vision beyond cardiology, and even outside of medicine.