Jinchao Feng
Data-Driven Model Selections of Second-Order Particle Dynamics via Integrating Gaussian Processes with Low-Dimensional Interacting Structures
Nov 01, 2023



Abstract:In this paper, we focus on the data-driven discovery of a general second-order particle-based model that contains many state-of-the-art models for modeling the aggregation and collective behavior of interacting agents of similar size and body type. This model takes the form of a high-dimensional system of ordinary differential equations parameterized by two interaction kernels that appraise the alignment of positions and velocities. We propose a Gaussian Process-based approach to this problem, where the unknown model parameters are marginalized by using two independent Gaussian Process (GP) priors on latent interaction kernels constrained to dynamics and observational data. This results in a nonparametric model for interacting dynamical systems that accounts for uncertainty quantification. We also develop acceleration techniques to improve scalability. Moreover, we perform a theoretical analysis to interpret the methodology and investigate the conditions under which the kernels can be recovered. We demonstrate the effectiveness of the proposed approach on various prototype systems, including the selection of the order of the systems and the types of interactions. In particular, we present applications to modeling two real-world fish motion datasets that display flocking and milling patterns up to 248 dimensions. Despite the use of small data sets, the GP-based approach learns an effective representation of the nonlinear dynamics in these spaces and outperforms competitor methods.
Learning Collective Behaviors from Observation
Nov 01, 2023Abstract:We present a review of a series of learning methods used to identify the structure of dynamical systems, aiming to understand emergent behaviors in complex systems of interacting agents. These methods not only offer theoretical guarantees of convergence but also demonstrate computational efficiency in handling high-dimensional observational data. They can manage observation data from both first- and second-order dynamical systems, accounting for observation/stochastic noise, complex interaction rules, missing interaction features, and real-world observations of interacting agent systems. The essence of developing such a series of learning methods lies in designing appropriate loss functions using the variational inverse problem approach, which inherently provides dimension reduction capabilities to our learning methods.
Learning Interaction Variables and Kernels from Observations of Agent-Based Systems
Aug 04, 2022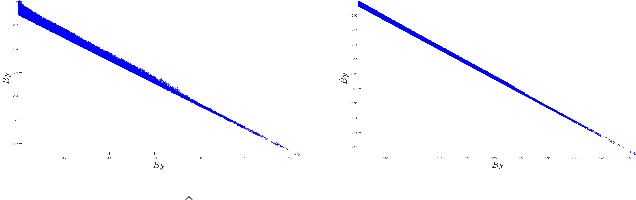
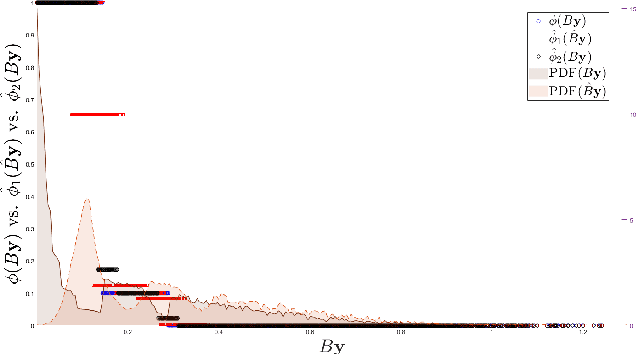

Abstract:Dynamical systems across many disciplines are modeled as interacting particles or agents, with interaction rules that depend on a very small number of variables (e.g. pairwise distances, pairwise differences of phases, etc...), functions of the state of pairs of agents. Yet, these interaction rules can generate self-organized dynamics, with complex emergent behaviors (clustering, flocking, swarming, etc.). We propose a learning technique that, given observations of states and velocities along trajectories of the agents, yields both the variables upon which the interaction kernel depends and the interaction kernel itself, in a nonparametric fashion. This yields an effective dimension reduction which avoids the curse of dimensionality from the high-dimensional observation data (states and velocities of all the agents). We demonstrate the learning capability of our method to a variety of first-order interacting systems.
Model Uncertainty and Correctability for Directed Graphical Models
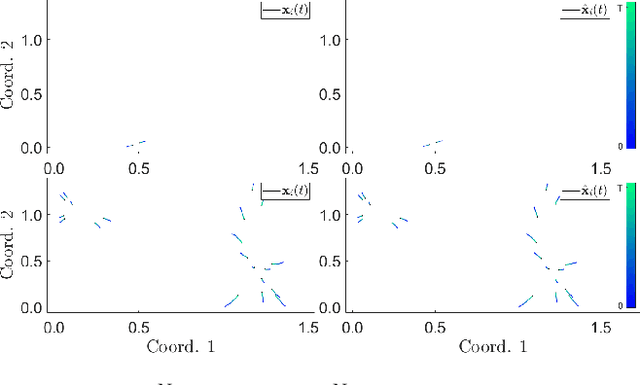
Jul 17, 2021
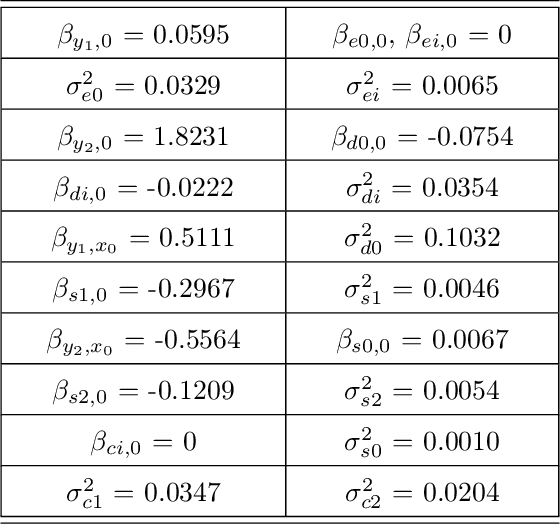


Abstract:Probabilistic graphical models are a fundamental tool in probabilistic modeling, machine learning and artificial intelligence. They allow us to integrate in a natural way expert knowledge, physical modeling, heterogeneous and correlated data and quantities of interest. For exactly this reason, multiple sources of model uncertainty are inherent within the modular structure of the graphical model. In this paper we develop information-theoretic, robust uncertainty quantification methods and non-parametric stress tests for directed graphical models to assess the effect and the propagation through the graph of multi-sourced model uncertainties to quantities of interest. These methods allow us to rank the different sources of uncertainty and correct the graphical model by targeting its most impactful components with respect to the quantities of interest. Thus, from a machine learning perspective, we provide a mathematically rigorous approach to correctability that guarantees a systematic selection for improvement of components of a graphical model while controlling potential new errors created in the process in other parts of the model. We demonstrate our methods in two physico-chemical examples, namely quantum scale-informed chemical kinetics and materials screening to improve the efficiency of fuel cells.
Data-driven discovery of interacting particle systems using Gaussian processes
Jun 04, 2021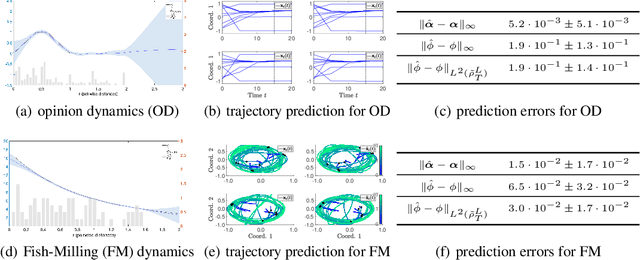



Abstract:Interacting particle or agent systems that display a rich variety of collection motions are ubiquitous in science and engineering. A fundamental and challenging goal is to understand the link between individual interaction rules and collective behaviors. In this paper, we study the data-driven discovery of distance-based interaction laws in second-order interacting particle systems. We propose a learning approach that models the latent interaction kernel functions as Gaussian processes, which can simultaneously fulfill two inference goals: one is the nonparametric inference of interaction kernel function with the pointwise uncertainty quantification, and the other one is the inference of unknown parameters in the non-collective forces of the system. We formulate learning interaction kernel functions as a statistical inverse problem and provide a detailed analysis of recoverability conditions, establishing that a coercivity condition is sufficient for recoverability. We provide a finite-sample analysis, showing that our posterior mean estimator converges at an optimal rate equal to the one in the classical 1-dimensional Kernel Ridge regression. Numerical results on systems that exhibit different collective behaviors demonstrate efficient learning of our approach from scarce noisy trajectory data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge