Control LLM: Controlled Evolution for Intelligence Retention in LLM

Large Language Models (LLMs) demand significant computational resources, making it essential to enhance their capabilities without retraining from scratch. A key challenge in this domain is \textit{catastrophic forgetting} (CF), which hampers performance during Continuous Pre-training (CPT) and Continuous Supervised Fine-Tuning (CSFT). We propose \textbf{Control LLM}, a novel approach that leverages parallel pre-trained and expanded transformer blocks, aligning their hidden-states through interpolation strategies This method effectively preserves performance on existing tasks while seamlessly integrating new knowledge. Extensive experiments demonstrate the effectiveness of Control LLM in both CPT and CSFT. On Llama3.1-8B-Instruct, it achieves significant improvements in mathematical reasoning ($+14.4\%$ on Math-Hard) and coding performance ($+10\%$ on MBPP-PLUS). On Llama3.1-8B, it enhances multilingual capabilities ($+10.6\%$ on C-Eval, $+6.8\%$ on CMMLU, and $+30.2\%$ on CMMLU-0shot-CoT). It surpasses existing methods and achieves SOTA among open-source models tuned from the same base model, using substantially less data and compute. Crucially, these gains are realized while preserving strong original capabilities, with minimal degradation ($<4.3\% \text{on MMLU}$) compared to $>35\%$ in open-source Math and Coding models. This approach has been successfully deployed in LinkedIn's GenAI-powered job seeker and Ads unit products. To support further research, we release the training and evaluation code (\url{https://github.com/linkedin/ControlLLM}) along with models trained on public datasets (\url{ https://huggingface.co/ControlLLM}) to the community.

Learning to Retrieve for Job Matching

Web-scale search systems typically tackle the scalability challenge with a two-step paradigm: retrieval and ranking. The retrieval step, also known as candidate selection, often involves extracting standardized entities, creating an inverted index, and performing term matching for retrieval. Such traditional methods require manual and time-consuming development of query models. In this paper, we discuss applying learning-to-retrieve technology to enhance LinkedIns job search and recommendation systems. In the realm of promoted jobs, the key objective is to improve the quality of applicants, thereby delivering value to recruiter customers. To achieve this, we leverage confirmed hire data to construct a graph that evaluates a seeker's qualification for a job, and utilize learned links for retrieval. Our learned model is easy to explain, debug, and adjust. On the other hand, the focus for organic jobs is to optimize seeker engagement. We accomplished this by training embeddings for personalized retrieval, fortified by a set of rules derived from the categorization of member feedback. In addition to a solution based on a conventional inverted index, we developed an on-GPU solution capable of supporting both KNN and term matching efficiently.

Data-driven discovery of interacting particle systems using Gaussian processes

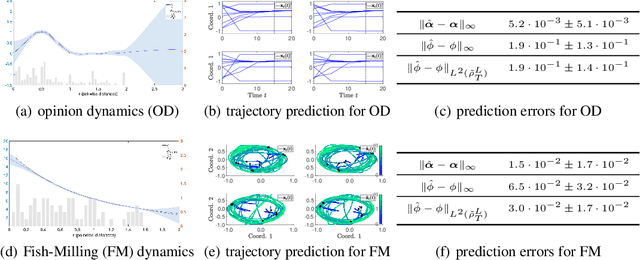
Interacting particle or agent systems that display a rich variety of collection motions are ubiquitous in science and engineering. A fundamental and challenging goal is to understand the link between individual interaction rules and collective behaviors. In this paper, we study the data-driven discovery of distance-based interaction laws in second-order interacting particle systems. We propose a learning approach that models the latent interaction kernel functions as Gaussian processes, which can simultaneously fulfill two inference goals: one is the nonparametric inference of interaction kernel function with the pointwise uncertainty quantification, and the other one is the inference of unknown parameters in the non-collective forces of the system. We formulate learning interaction kernel functions as a statistical inverse problem and provide a detailed analysis of recoverability conditions, establishing that a coercivity condition is sufficient for recoverability. We provide a finite-sample analysis, showing that our posterior mean estimator converges at an optimal rate equal to the one in the classical 1-dimensional Kernel Ridge regression. Numerical results on systems that exhibit different collective behaviors demonstrate efficient learning of our approach from scarce noisy trajectory data.