RandONet: Shallow-Networks with Random Projections for learning linear and nonlinear operators
Paper and Code
Jun 08, 2024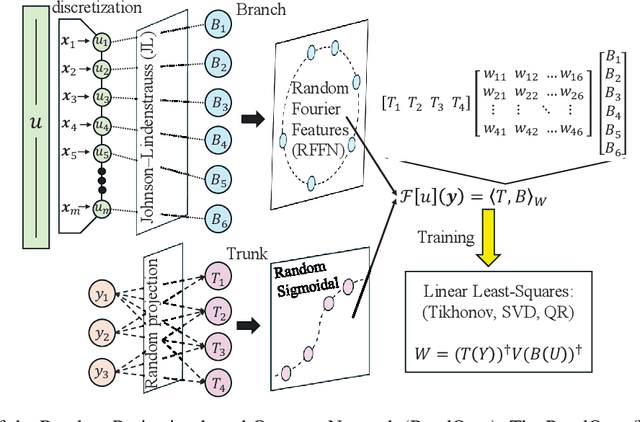
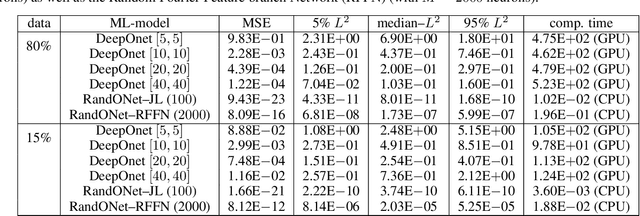
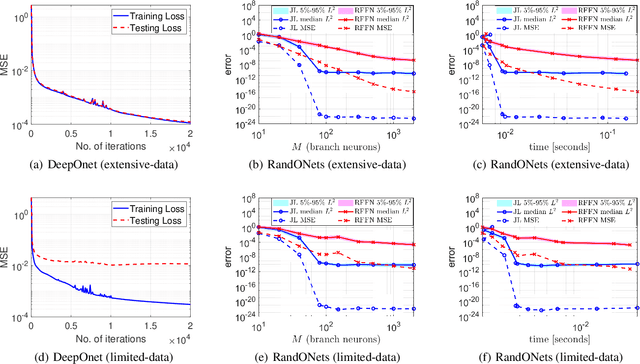
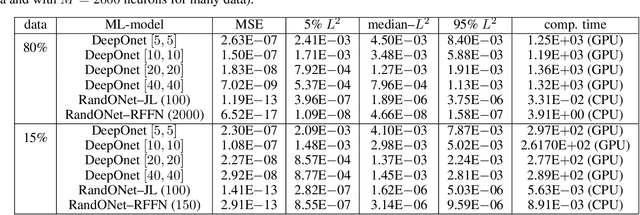
Deep Operator Networks (DeepOnets) have revolutionized the domain of scientific machine learning for the solution of the inverse problem for dynamical systems. However, their implementation necessitates optimizing a high-dimensional space of parameters and hyperparameters. This fact, along with the requirement of substantial computational resources, poses a barrier to achieving high numerical accuracy. Here, inpsired by DeepONets and to address the above challenges, we present Random Projection-based Operator Networks (RandONets): shallow networks with random projections that learn linear and nonlinear operators. The implementation of RandONets involves: (a) incorporating random bases, thus enabling the use of shallow neural networks with a single hidden layer, where the only unknowns are the output weights of the network's weighted inner product; this reduces dramatically the dimensionality of the parameter space; and, based on this, (b) using established least-squares solvers (e.g., Tikhonov regularization and preconditioned QR decomposition) that offer superior numerical approximation properties compared to other optimization techniques used in deep-learning. In this work, we prove the universal approximation accuracy of RandONets for approximating nonlinear operators and demonstrate their efficiency in approximating linear nonlinear evolution operators (right-hand-sides (RHS)) with a focus on PDEs. We show, that for this particular task, RandONets outperform, both in terms of numerical approximation accuracy and computational cost, the ``vanilla" DeepOnets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge