Stability Analysis of Physics-Informed Neural Networks for Stiff Linear Differential Equations

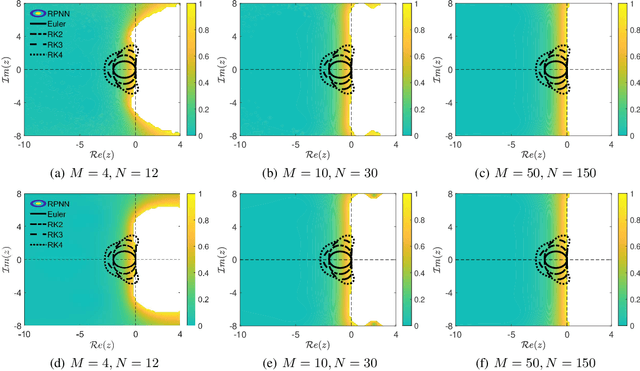
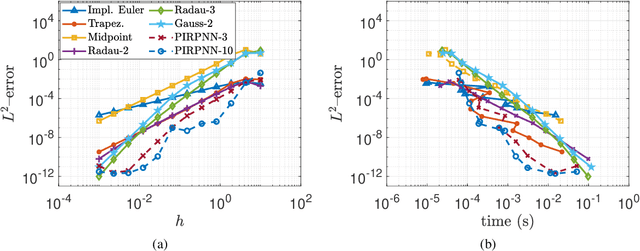
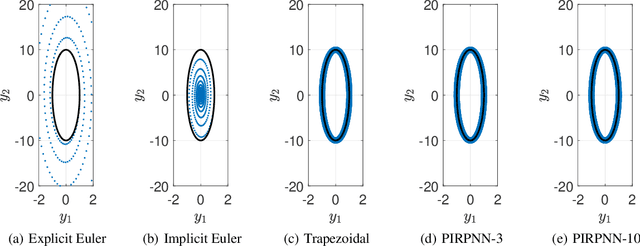
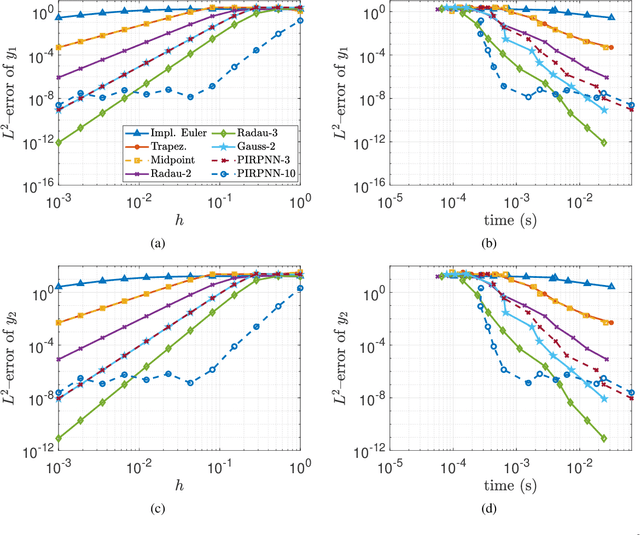
We present a stability analysis of Physics-Informed Neural Networks (PINNs) coupled with random projections, for the numerical solution of (stiff) linear differential equations. For our analysis, we consider systems of linear ODEs, and linear parabolic PDEs. We prove that properly designed PINNs offer consistent and asymptotically stable numerical schemes, thus convergent schemes. In particular, we prove that multi-collocation random projection PINNs guarantee asymptotic stability for very high stiffness and that single-collocation PINNs are $A$-stable. To assess the performance of the PINNs in terms of both numerical approximation accuracy and computational cost, we compare it with other implicit schemes and in particular backward Euler, the midpoint, trapezoidal (Crank-Nikolson), the 2-stage Gauss scheme and the 2 and 3 stages Radau schemes. We show that the proposed PINNs outperform the above traditional schemes, in both numerical approximation accuracy and importantly computational cost, for a wide range of step sizes.

RandONet: Shallow-Networks with Random Projections for learning linear and nonlinear operators

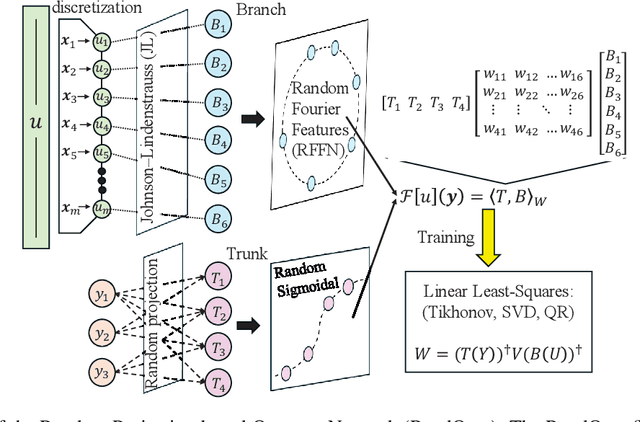
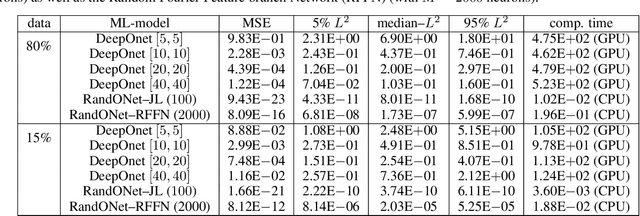
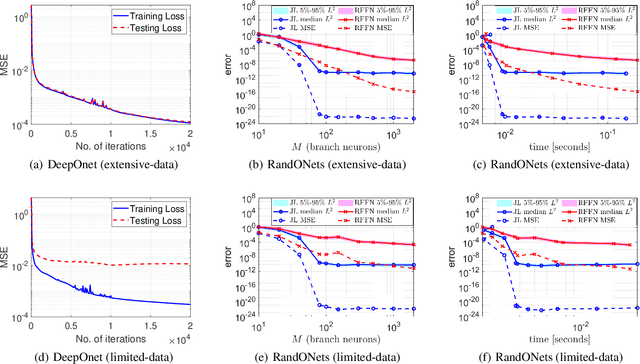
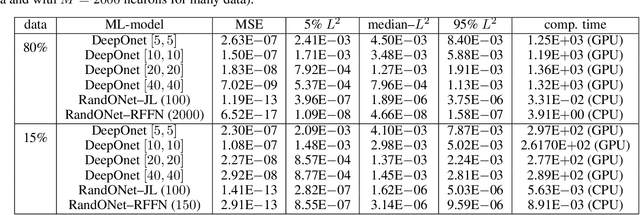
Deep Operator Networks (DeepOnets) have revolutionized the domain of scientific machine learning for the solution of the inverse problem for dynamical systems. However, their implementation necessitates optimizing a high-dimensional space of parameters and hyperparameters. This fact, along with the requirement of substantial computational resources, poses a barrier to achieving high numerical accuracy. Here, inpsired by DeepONets and to address the above challenges, we present Random Projection-based Operator Networks (RandONets): shallow networks with random projections that learn linear and nonlinear operators. The implementation of RandONets involves: (a) incorporating random bases, thus enabling the use of shallow neural networks with a single hidden layer, where the only unknowns are the output weights of the network's weighted inner product; this reduces dramatically the dimensionality of the parameter space; and, based on this, (b) using established least-squares solvers (e.g., Tikhonov regularization and preconditioned QR decomposition) that offer superior numerical approximation properties compared to other optimization techniques used in deep-learning. In this work, we prove the universal approximation accuracy of RandONets for approximating nonlinear operators and demonstrate their efficiency in approximating linear nonlinear evolution operators (right-hand-sides (RHS)) with a focus on PDEs. We show, that for this particular task, RandONets outperform, both in terms of numerical approximation accuracy and computational cost, the ``vanilla" DeepOnets.

Statistical monitoring of functional data using the notion of Fréchet mean combined with the framework of the deformation models

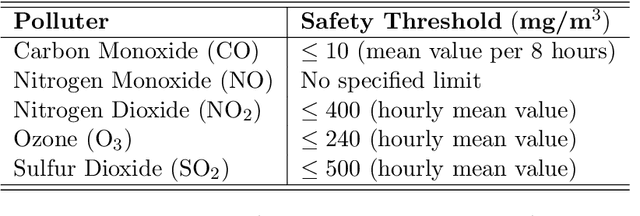
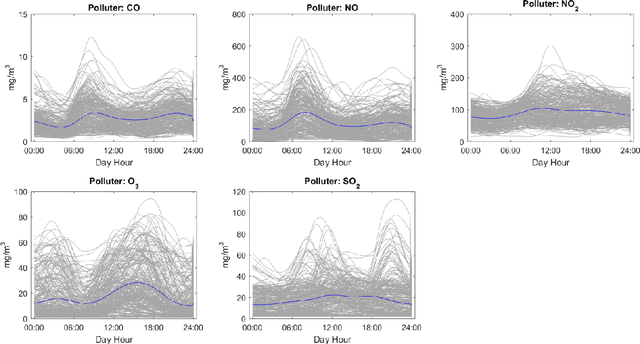
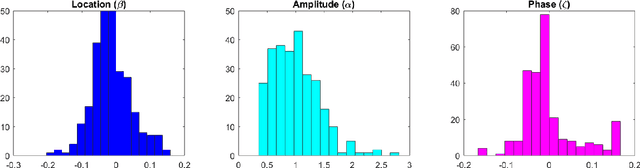
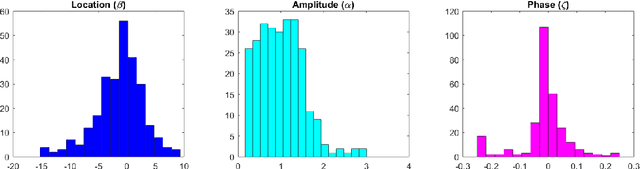
The aim of this paper is to investigate possible advances obtained by the implementation of the framework of Fr\'echet mean and the generalized sense of mean that it offers, in the field of statistical process monitoring and control. In particular, the case of non-linear profiles which are described by data in functional form is considered and a framework combining the notion of Fr\'echet mean and deformation models is developed. The proposed monitoring approach is implemented to the intra-day air pollution monitoring task in the city of Athens where the capabilities and advantages of the method are illustrated.