Conformalized Polynomial Chaos Expansion for Uncertainty-aware Surrogate Modeling

This work introduces a method to equip data-driven polynomial chaos expansion surrogate models with intervals that quantify the predictive uncertainty of the surrogate. To that end, we integrate jackknife-based conformal prediction into regression-based polynomial chaos expansions. The jackknife algorithm uses leave-one-out residuals to generate predictive intervals around the predictions of the polynomial chaos surrogate. The jackknife+ extension additionally requires leave-one-out model predictions. The key to efficient implementation is to leverage the linearity of the polynomial chaos regression model, so that leave-one-out residuals and, if necessary, leave-one-out model predictions can be computed with analytical, closed-form expressions, thus eliminating the need for repeated model re-training. In addition to the efficient computation of the predictive intervals, a significant advantage of this approach is its data efficiency, as it requires no hold-out dataset for prediction interval calibration, thus allowing the entire dataset to be used for model training. The conformalized polynomial chaos expansion method is validated on several benchmark models, where the impact of training data volume on the predictive intervals is additionally investigated.

Generative Learning for Slow Manifolds and Bifurcation Diagrams

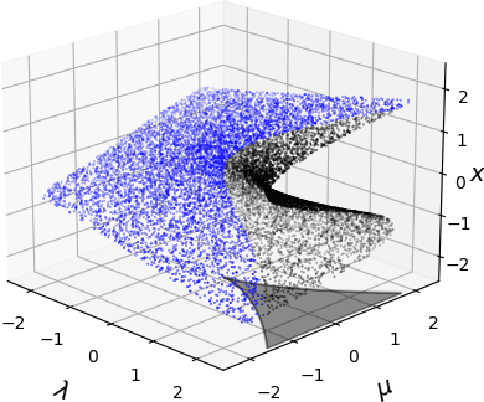
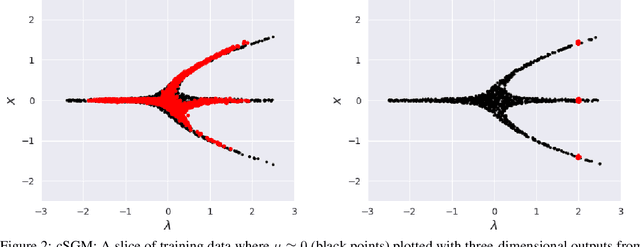
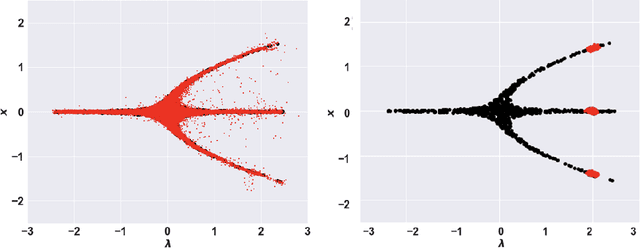
In dynamical systems characterized by separation of time scales, the approximation of so called ``slow manifolds'', on which the long term dynamics lie, is a useful step for model reduction. Initializing on such slow manifolds is a useful step in modeling, since it circumvents fast transients, and is crucial in multiscale algorithms alternating between fine scale (fast) and coarser scale (slow) simulations. In a similar spirit, when one studies the infinite time dynamics of systems depending on parameters, the system attractors (e.g., its steady states) lie on bifurcation diagrams. Sampling these manifolds gives us representative attractors (here, steady states of ODEs or PDEs) at different parameter values. Algorithms for the systematic construction of these manifolds are required parts of the ``traditional'' numerical nonlinear dynamics toolkit. In more recent years, as the field of Machine Learning develops, conditional score-based generative models (cSGMs) have demonstrated capabilities in generating plausible data from target distributions that are conditioned on some given label. It is tempting to exploit such generative models to produce samples of data distributions conditioned on some quantity of interest (QoI). In this work, we present a framework for using cSGMs to quickly (a) initialize on a low-dimensional (reduced-order) slow manifold of a multi-time-scale system consistent with desired value(s) of a QoI (a ``label'') on the manifold, and (b) approximate steady states in a bifurcation diagram consistent with a (new, out-of-sample) parameter value. This conditional sampling can help uncover the geometry of the reduced slow-manifold and/or approximately ``fill in'' missing segments of steady states in a bifurcation diagram.

Generative Learning of Densities on Manifolds

A generative modeling framework is proposed that combines diffusion models and manifold learning to efficiently sample data densities on manifolds. The approach utilizes Diffusion Maps to uncover possible low-dimensional underlying (latent) spaces in the high-dimensional data (ambient) space. Two approaches for sampling from the latent data density are described. The first is a score-based diffusion model, which is trained to map a standard normal distribution to the latent data distribution using a neural network. The second one involves solving an It\^o stochastic differential equation in the latent space. Additional realizations of the data are generated by lifting the samples back to the ambient space using Double Diffusion Maps, a recently introduced technique typically employed in studying dynamical system reduction; here the focus lies in sampling densities rather than system dynamics. The proposed approaches enable sampling high dimensional data densities restricted to low-dimensional, a priori unknown manifolds. The efficacy of the proposed framework is demonstrated through a benchmark problem and a material with multiscale structure.

Polynomial Chaos Expansions on Principal Geodesic Grassmannian Submanifolds for Surrogate Modeling and Uncertainty Quantification

In this work we introduce a manifold learning-based surrogate modeling framework for uncertainty quantification in high-dimensional stochastic systems. Our first goal is to perform data mining on the available simulation data to identify a set of low-dimensional (latent) descriptors that efficiently parameterize the response of the high-dimensional computational model. To this end, we employ Principal Geodesic Analysis on the Grassmann manifold of the response to identify a set of disjoint principal geodesic submanifolds, of possibly different dimension, that captures the variation in the data. Since operations on the Grassmann require the data to be concentrated, we propose an adaptive algorithm based on Riemanniann K-means and the minimization of the sample Frechet variance on the Grassmann manifold to identify "local" principal geodesic submanifolds that represent different system behavior across the parameter space. Polynomial chaos expansion is then used to construct a mapping between the random input parameters and the projection of the response on these local principal geodesic submanifolds. The method is demonstrated on four test cases, a toy-example that involves points on a hypersphere, a Lotka-Volterra dynamical system, a continuous-flow stirred-tank chemical reactor system, and a two-dimensional Rayleigh-Benard convection problem

Data-driven Uncertainty Quantification in Computational Human Head Models

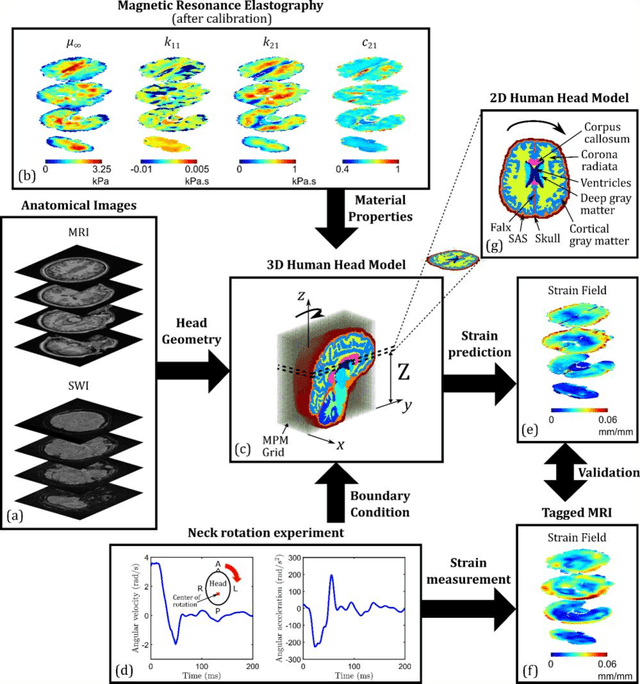
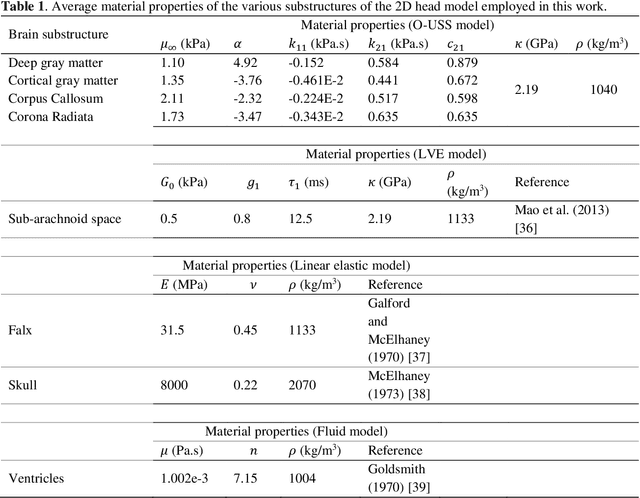
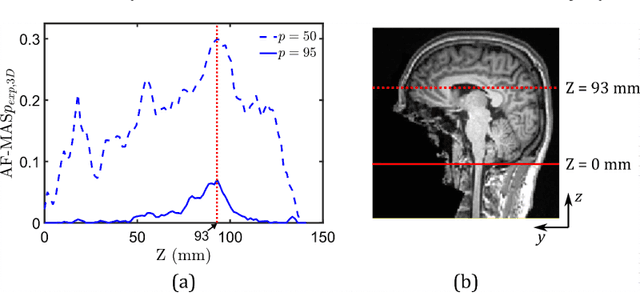
Computational models of the human head are promising tools for estimating the impact-induced response of brain, and thus play an important role in the prediction of traumatic brain injury. Modern biofidelic head model simulations are associated with very high computational cost, and high-dimensional inputs and outputs, which limits the applicability of traditional uncertainty quantification (UQ) methods on these systems. In this study, a two-stage, data-driven manifold learning-based framework is proposed for UQ of computational head models. This framework is demonstrated on a 2D subject-specific head model, where the goal is to quantify uncertainty in the simulated strain fields (i.e., output), given variability in the material properties of different brain substructures (i.e., input). In the first stage, a data-driven method based on multi-dimensional Gaussian kernel-density estimation and diffusion maps is used to generate realizations of the input random vector directly from the available data. Computational simulations of a small number of realizations provide input-output pairs for training data-driven surrogate models in the second stage. The surrogate models employ nonlinear dimensionality reduction using Grassmannian diffusion maps, Gaussian process regression to create a low-cost mapping between the input random vector and the reduced solution space, and geometric harmonics models for mapping between the reduced space and the Grassmann manifold. It is demonstrated that the surrogate models provide highly accurate approximations of the computational model while significantly reducing the computational cost. Monte Carlo simulations of the surrogate models are used for uncertainty propagation. UQ of strain fields highlight significant spatial variation in model uncertainty, and reveal key differences in uncertainty among commonly used strain-based brain injury predictor variables.