Data-driven Uncertainty Quantification in Computational Human Head Models
Paper and Code
Oct 29, 2021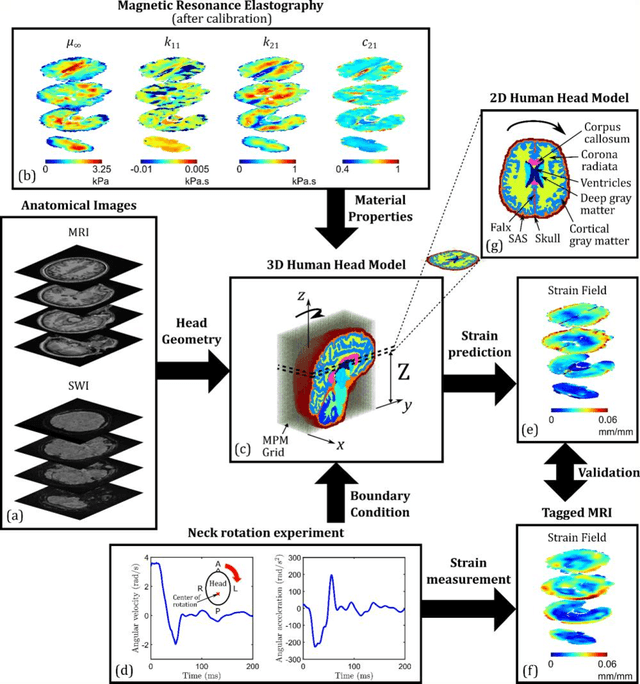
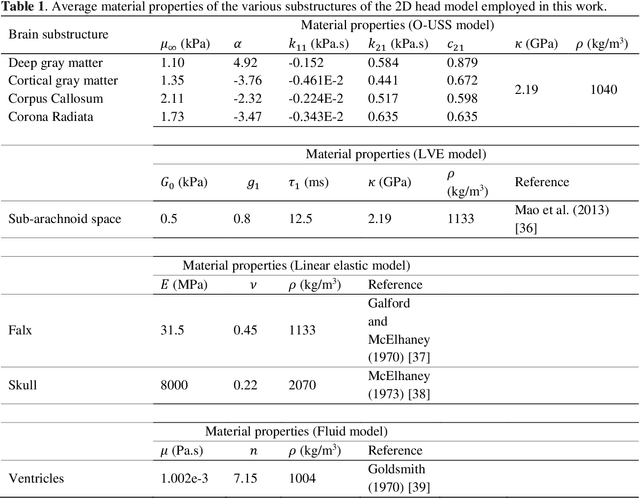
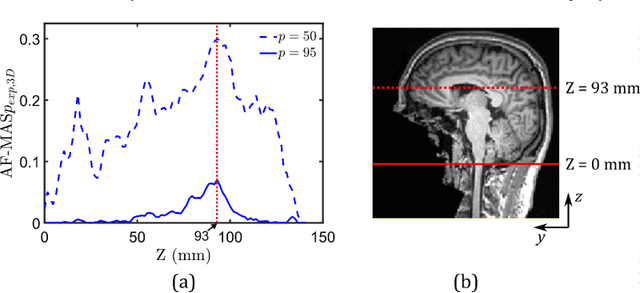

Computational models of the human head are promising tools for estimating the impact-induced response of brain, and thus play an important role in the prediction of traumatic brain injury. Modern biofidelic head model simulations are associated with very high computational cost, and high-dimensional inputs and outputs, which limits the applicability of traditional uncertainty quantification (UQ) methods on these systems. In this study, a two-stage, data-driven manifold learning-based framework is proposed for UQ of computational head models. This framework is demonstrated on a 2D subject-specific head model, where the goal is to quantify uncertainty in the simulated strain fields (i.e., output), given variability in the material properties of different brain substructures (i.e., input). In the first stage, a data-driven method based on multi-dimensional Gaussian kernel-density estimation and diffusion maps is used to generate realizations of the input random vector directly from the available data. Computational simulations of a small number of realizations provide input-output pairs for training data-driven surrogate models in the second stage. The surrogate models employ nonlinear dimensionality reduction using Grassmannian diffusion maps, Gaussian process regression to create a low-cost mapping between the input random vector and the reduced solution space, and geometric harmonics models for mapping between the reduced space and the Grassmann manifold. It is demonstrated that the surrogate models provide highly accurate approximations of the computational model while significantly reducing the computational cost. Monte Carlo simulations of the surrogate models are used for uncertainty propagation. UQ of strain fields highlight significant spatial variation in model uncertainty, and reveal key differences in uncertainty among commonly used strain-based brain injury predictor variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge