Centralized Fairness for Redistricting
Paper and Code
Mar 02, 2022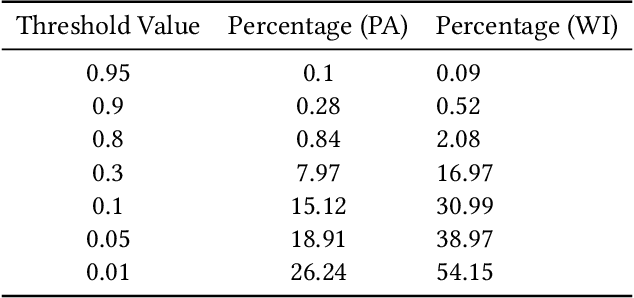
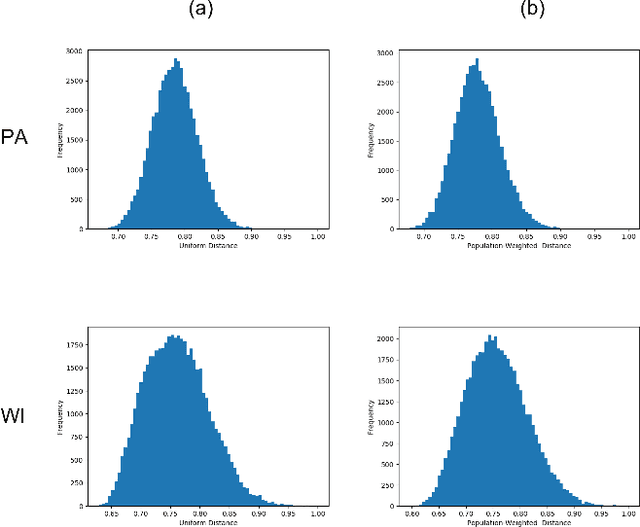
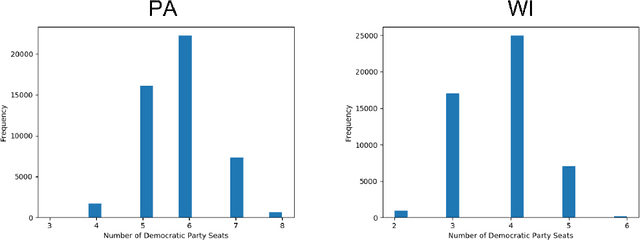
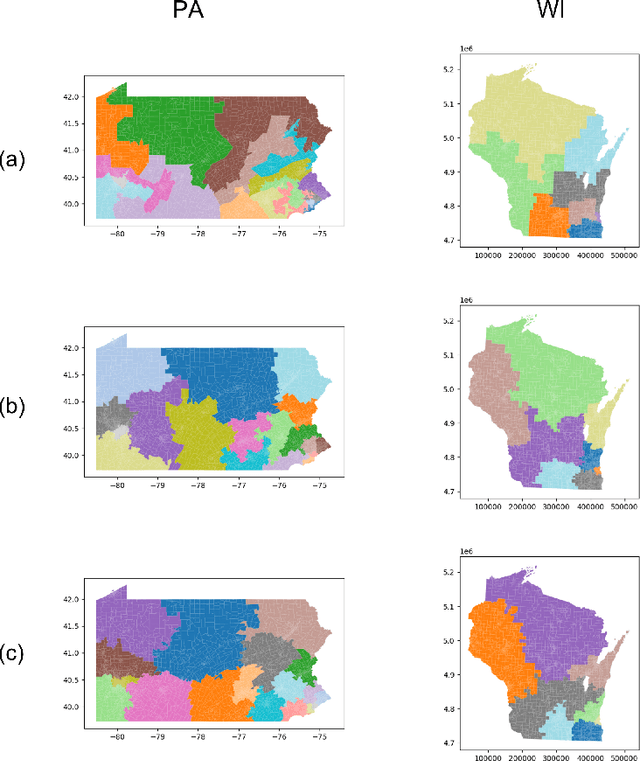
In representative democracy, the electorate is often partitioned into districts with each district electing a representative. However, these systems have proven vulnerable to the practice of partisan gerrymandering which involves drawing districts that elect more representatives from a given political party. Additionally, computer-based methods have dramatically enhanced the ability to draw districts that drastically favor one party over others. On the positive side, researchers have recently developed tools for measuring how gerrymandered a redistricting map is by comparing it to a large set of randomly-generated district maps. While these efforts to test whether a district map is "gerrymandered" have achieved real-world impact, the question of how best to draw districts remains very open. Many attempts to automate the redistricting process have been proposed, but not adopted into practice. Typically, they have focused on optimizing certain properties (e.g., geographical compactness or partisan competitiveness of districts) and argued that the properties are desirable. In this work, we take an alternative approach which seeks to find the most "typical" redistricting map. More precisely, we introduce a family of well-motivated distance measures over redistricting maps. Then, by generating a large collection of maps using sampling techniques, we select the map which minimizes the sum of the distances from the collection, i.e., the most "central" map. We produce scalable, linear-time algorithms and derive sample complexity guarantees. Empirically, we show the validity of our algorithms over real world redistricting problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge