Probabilistic Fair Clustering
Paper and Code
Jun 19, 2020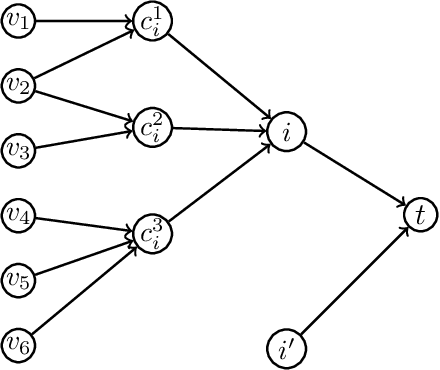
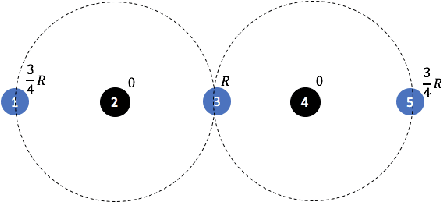
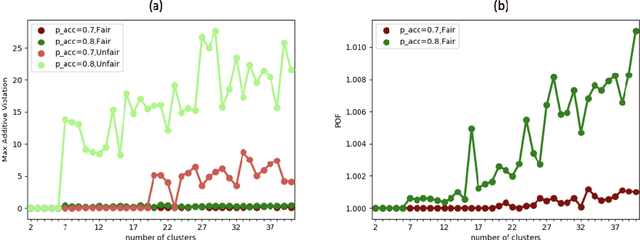
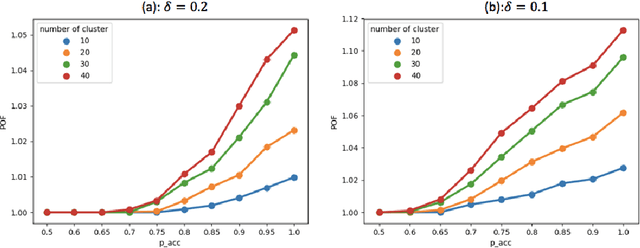
In clustering problems, a central decision-maker is given a complete metric graph over vertices and must provide a clustering of vertices that minimizes some objective function. In fair clustering problems, vertices are endowed with a color (e.g., membership in a group), and the features of a valid clustering might also include the representation of colors in that clustering. Prior work in fair clustering assumes complete knowledge of group membership. In this paper, we generalize prior work by assuming imperfect knowledge of group membership through probabilistic assignments. We present clustering algorithms in this more general setting with approximation ratio guarantees. We also address the problem of "metric membership", where different groups have a notion of order and distance. Experiments are conducted using our proposed algorithms as well as baselines to validate our approach and also surface nuanced concerns when group membership is not known deterministically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge