On Correcting Inputs: Inverse Optimization for Online Structured Prediction
Paper and Code
Oct 12, 2015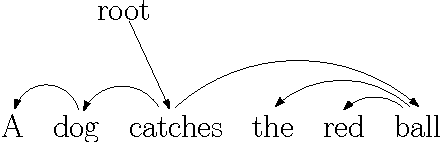
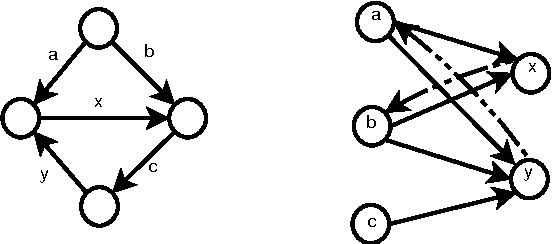
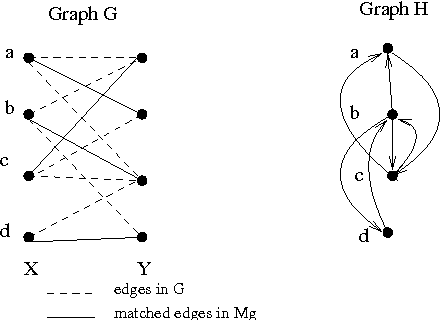
Algorithm designers typically assume that the input data is correct, and then proceed to find "optimal" or "sub-optimal" solutions using this input data. However this assumption of correct data does not always hold in practice, especially in the context of online learning systems where the objective is to learn appropriate feature weights given some training samples. Such scenarios necessitate the study of inverse optimization problems where one is given an input instance as well as a desired output and the task is to adjust the input data so that the given output is indeed optimal. Motivated by learning structured prediction models, in this paper we consider inverse optimization with a margin, i.e., we require the given output to be better than all other feasible outputs by a desired margin. We consider such inverse optimization problems for maximum weight matroid basis, matroid intersection, perfect matchings, minimum cost maximum flows, and shortest paths and derive the first known results for such problems with a non-zero margin. The effectiveness of these algorithmic approaches to online learning for structured prediction is also discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge