The Complexity of Manipulation of k-Coalitional Games on Graphs

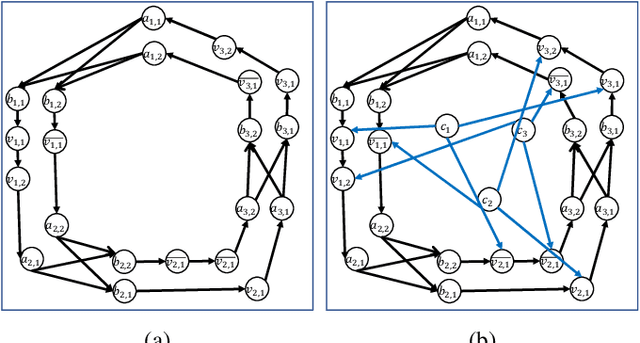
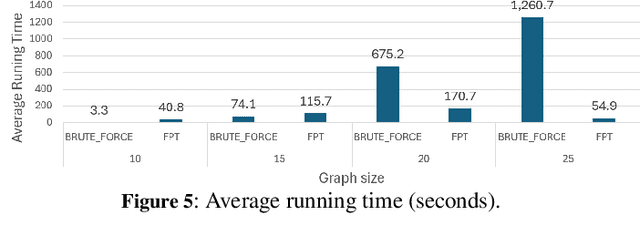
In many settings, there is an organizer who would like to divide a set of agents into $k$ coalitions, and cares about the friendships within each coalition. Specifically, the organizer might want to maximize utilitarian social welfare, maximize egalitarian social welfare, or simply guarantee that every agent will have at least one friend within his coalition. However, in many situations, the organizer is not familiar with the friendship connections, and he needs to obtain them from the agents. In this setting, a manipulative agent may falsely report friendship connections in order to increase his utility. In this paper, we analyze the complexity of finding manipulation in such $k$-coalitional games on graphs. We also introduce a new type of manipulation, socially-aware manipulation, in which the manipulator would like to increase his utility without decreasing the social welfare. We then study the complexity of finding socially-aware manipulation in our setting. Finally, we examine the frequency of socially-aware manipulation and the running time of our algorithms via simulation results.

Resource Sharing Through Multi-Round Matchings

Applications such as employees sharing office spaces over a workweek can be modeled as problems where agents are matched to resources over multiple rounds. Agents' requirements limit the set of compatible resources and the rounds in which they want to be matched. Viewing such an application as a multi-round matching problem on a bipartite compatibility graph between agents and resources, we show that a solution (i.e., a set of matchings, with one matching per round) can be found efficiently if one exists. To cope with situations where a solution does not exist, we consider two extensions. In the first extension, a benefit function is defined for each agent and the objective is to find a multi-round matching to maximize the total benefit. For a general class of benefit functions satisfying certain properties (including diminishing returns), we show that this multi-round matching problem is efficiently solvable. This class includes utilitarian and Rawlsian welfare functions. For another benefit function, we show that the maximization problem is NP-hard. In the second extension, the objective is to generate advice to each agent (i.e., a subset of requirements to be relaxed) subject to a budget constraint so that the agent can be matched. We show that this budget-constrained advice generation problem is NP-hard. For this problem, we develop an integer linear programming formulation as well as a heuristic based on local search. We experimentally evaluate our algorithms on synthetic networks and apply them to two real-world situations: shared office spaces and matching courses to classrooms.

Resource Allocation to Agents with Restrictions: Maximizing Likelihood with Minimum Compromise

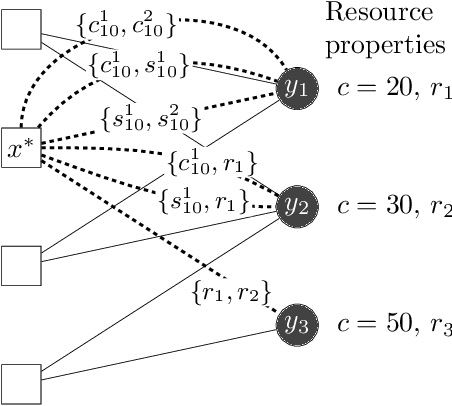
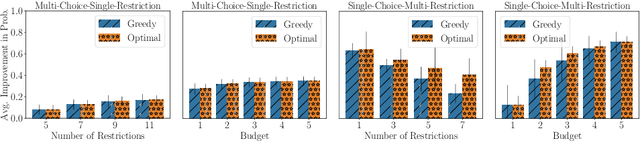
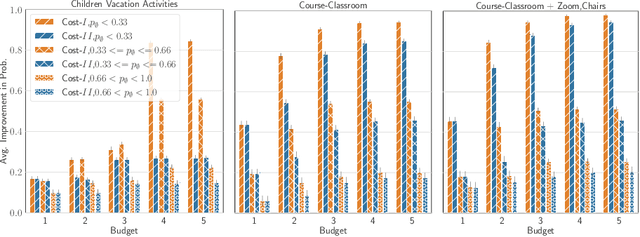
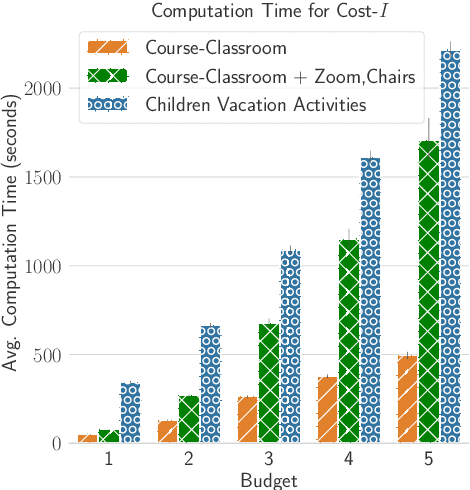
Many scenarios where agents with restrictions compete for resources can be cast as maximum matching problems on bipartite graphs. Our focus is on resource allocation problems where agents may have restrictions that make them incompatible with some resources. We assume that a Principle chooses a maximum matching randomly so that each agent is matched to a resource with some probability. Agents would like to improve their chances of being matched by modifying their restrictions within certain limits. The Principle's goal is to advise an unsatisfied agent to relax its restrictions so that the total cost of relaxation is within a budget (chosen by the agent) and the increase in the probability of being assigned a resource is maximized. We establish hardness results for some variants of this budget-constrained maximization problem and present algorithmic results for other variants. We experimentally evaluate our methods on synthetic datasets as well as on two novel real-world datasets: a vacation activities dataset and a classrooms dataset.