IGraSS: Learning to Identify Infrastructure Networks from Satellite Imagery by Iterative Graph-constrained Semantic Segmentation

Accurate canal network mapping is essential for water management, including irrigation planning and infrastructure maintenance. State-of-the-art semantic segmentation models for infrastructure mapping, such as roads, rely on large, well-annotated remote sensing datasets. However, incomplete or inadequate ground truth can hinder these learning approaches. Many infrastructure networks have graph-level properties such as reachability to a source (like canals) or connectivity (roads) that can be leveraged to improve these existing ground truth. This paper develops a novel iterative framework IGraSS, combining a semantic segmentation module-incorporating RGB and additional modalities (NDWI, DEM)-with a graph-based ground-truth refinement module. The segmentation module processes satellite imagery patches, while the refinement module operates on the entire data viewing the infrastructure network as a graph. Experiments show that IGraSS reduces unreachable canal segments from around 18% to 3%, and training with refined ground truth significantly improves canal identification. IGraSS serves as a robust framework for both refining noisy ground truth and mapping canal networks from remote sensing imagery. We also demonstrate the effectiveness and generalizability of IGraSS using road networks as an example, applying a different graph-theoretic constraint to complete road networks.

Knowledge-Informed Deep Learning for Irrigation Type Mapping from Remote Sensing

Accurate mapping of irrigation methods is crucial for sustainable agricultural practices and food systems. However, existing models that rely solely on spectral features from satellite imagery are ineffective due to the complexity of agricultural landscapes and limited training data, making this a challenging problem. We present Knowledge-Informed Irrigation Mapping (KIIM), a novel Swin-Transformer based approach that uses (i) a specialized projection matrix to encode crop to irrigation probability, (ii) a spatial attention map to identify agricultural lands from non-agricultural lands, (iii) bi-directional cross-attention to focus complementary information from different modalities, and (iv) a weighted ensemble for combining predictions from images and crop information. Our experimentation on five states in the US shows up to 22.9\% (IoU) improvement over baseline with a 71.4% (IoU) improvement for hard-to-classify drip irrigation. In addition, we propose a two-phase transfer learning approach to enhance cross-state irrigation mapping, achieving a 51% IoU boost in a state with limited labeled data. The ability to achieve baseline performance with only 40% of the training data highlights its efficiency, reducing the dependency on extensive manual labeling efforts and making large-scale, automated irrigation mapping more feasible and cost-effective.

IrrMap: A Large-Scale Comprehensive Dataset for Irrigation Method Mapping

We introduce IrrMap, the first large-scale dataset (1.1 million patches) for irrigation method mapping across regions. IrrMap consists of multi-resolution satellite imagery from LandSat and Sentinel, along with key auxiliary data such as crop type, land use, and vegetation indices. The dataset spans 1,687,899 farms and 14,117,330 acres across multiple western U.S. states from 2013 to 2023, providing a rich and diverse foundation for irrigation analysis and ensuring geospatial alignment and quality control. The dataset is ML-ready, with standardized 224x224 GeoTIFF patches, the multiple input modalities, carefully chosen train-test-split data, and accompanying dataloaders for seamless deep learning model training andbenchmarking in irrigation mapping. The dataset is also accompanied by a complete pipeline for dataset generation, enabling researchers to extend IrrMap to new regions for irrigation data collection or adapt it with minimal effort for other similar applications in agricultural and geospatial analysis. We also analyze the irrigation method distribution across crop groups, spatial irrigation patterns (using Shannon diversity indices), and irrigated area variations for both LandSat and Sentinel, providing insights into regional and resolution-based differences. To promote further exploration, we openly release IrrMap, along with the derived datasets, benchmark models, and pipeline code, through a GitHub repository: https://github.com/Nibir088/IrrMap and Data repository: https://huggingface.co/Nibir/IrrMap, providing comprehensive documentation and implementation details.

A Unifying Information-theoretic Perspective on Evaluating Generative Models

Considering the difficulty of interpreting generative model output, there is significant current research focused on determining meaningful evaluation metrics. Several recent approaches utilize "precision" and "recall," borrowed from the classification domain, to individually quantify the output fidelity (realism) and output diversity (representation of the real data variation), respectively. With the increase in metric proposals, there is a need for a unifying perspective, allowing for easier comparison and clearer explanation of their benefits and drawbacks. To this end, we unify a class of kth-nearest-neighbors (kNN)-based metrics under an information-theoretic lens using approaches from kNN density estimation. Additionally, we propose a tri-dimensional metric composed of Precision Cross-Entropy (PCE), Recall Cross-Entropy (RCE), and Recall Entropy (RE), which separately measure fidelity and two distinct aspects of diversity, inter- and intra-class. Our domain-agnostic metric, derived from the information-theoretic concepts of entropy and cross-entropy, can be dissected for both sample- and mode-level analysis. Our detailed experimental results demonstrate the sensitivity of our metric components to their respective qualities and reveal undesirable behaviors of other metrics.

Efficient PAC Learnability of Dynamical Systems Over Multilayer Networks

Networked dynamical systems are widely used as formal models of real-world cascading phenomena, such as the spread of diseases and information. Prior research has addressed the problem of learning the behavior of an unknown dynamical system when the underlying network has a single layer. In this work, we study the learnability of dynamical systems over multilayer networks, which are more realistic and challenging. First, we present an efficient PAC learning algorithm with provable guarantees to show that the learner only requires a small number of training examples to infer an unknown system. We further provide a tight analysis of the Natarajan dimension which measures the model complexity. Asymptotically, our bound on the Nararajan dimension is tight for almost all multilayer graphs. The techniques and insights from our work provide the theoretical foundations for future investigations of learning problems for multilayer dynamical systems.

IrrNet: Advancing Irrigation Mapping with Incremental Patch Size Training on Remote Sensing Imagery

Irrigation mapping plays a crucial role in effective water management, essential for preserving both water quality and quantity, and is key to mitigating the global issue of water scarcity. The complexity of agricultural fields, adorned with diverse irrigation practices, especially when multiple systems coexist in close quarters, poses a unique challenge. This complexity is further compounded by the nature of Landsat's remote sensing data, where each pixel is rich with densely packed information, complicating the task of accurate irrigation mapping. In this study, we introduce an innovative approach that employs a progressive training method, which strategically increases patch sizes throughout the training process, utilizing datasets from Landsat 5 and 7, labeled with the WRLU dataset for precise labeling. This initial focus allows the model to capture detailed features, progressively shifting to broader, more general features as the patch size enlarges. Remarkably, our method enhances the performance of existing state-of-the-art models by approximately 20%. Furthermore, our analysis delves into the significance of incorporating various spectral bands into the model, assessing their impact on performance. The findings reveal that additional bands are instrumental in enabling the model to discern finer details more effectively. This work sets a new standard for leveraging remote sensing imagery in irrigation mapping.

Learning the Topology and Behavior of Discrete Dynamical Systems

Discrete dynamical systems are commonly used to model the spread of contagions on real-world networks. Under the PAC framework, existing research has studied the problem of learning the behavior of a system, assuming that the underlying network is known. In this work, we focus on a more challenging setting: to learn both the behavior and the underlying topology of a black-box system. We show that, in general, this learning problem is computationally intractable. On the positive side, we present efficient learning methods under the PAC model when the underlying graph of the dynamical system belongs to some classes. Further, we examine a relaxed setting where the topology of an unknown system is partially observed. For this case, we develop an efficient PAC learner to infer the system and establish the sample complexity. Lastly, we present a formal analysis of the expressive power of the hypothesis class of dynamical systems where both the topology and behavior are unknown, using the well-known formalism of the Natarajan dimension. Our results provide a theoretical foundation for learning both the behavior and topology of discrete dynamical systems.

Resource Sharing Through Multi-Round Matchings

Applications such as employees sharing office spaces over a workweek can be modeled as problems where agents are matched to resources over multiple rounds. Agents' requirements limit the set of compatible resources and the rounds in which they want to be matched. Viewing such an application as a multi-round matching problem on a bipartite compatibility graph between agents and resources, we show that a solution (i.e., a set of matchings, with one matching per round) can be found efficiently if one exists. To cope with situations where a solution does not exist, we consider two extensions. In the first extension, a benefit function is defined for each agent and the objective is to find a multi-round matching to maximize the total benefit. For a general class of benefit functions satisfying certain properties (including diminishing returns), we show that this multi-round matching problem is efficiently solvable. This class includes utilitarian and Rawlsian welfare functions. For another benefit function, we show that the maximization problem is NP-hard. In the second extension, the objective is to generate advice to each agent (i.e., a subset of requirements to be relaxed) subject to a budget constraint so that the agent can be matched. We show that this budget-constrained advice generation problem is NP-hard. For this problem, we develop an integer linear programming formulation as well as a heuristic based on local search. We experimentally evaluate our algorithms on synthetic networks and apply them to two real-world situations: shared office spaces and matching courses to classrooms.

Resource Allocation to Agents with Restrictions: Maximizing Likelihood with Minimum Compromise

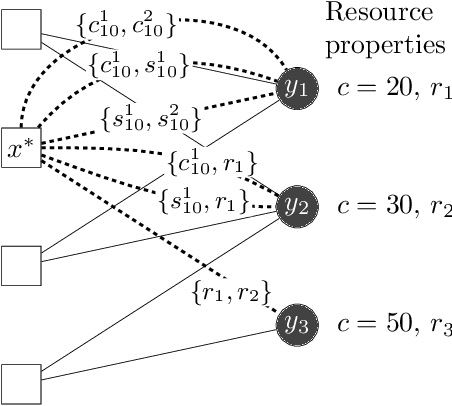
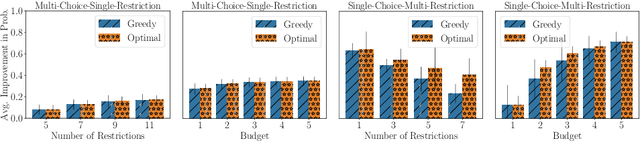
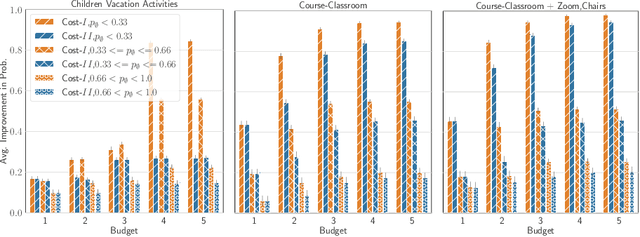
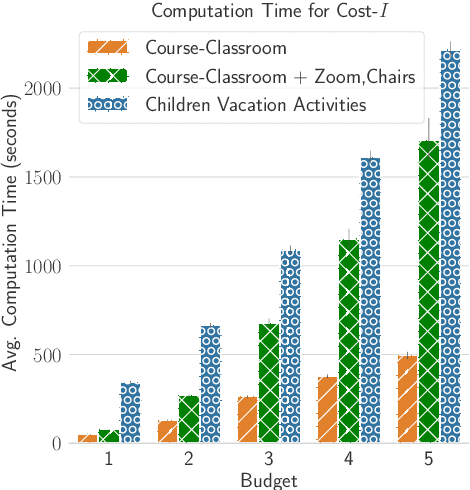
Many scenarios where agents with restrictions compete for resources can be cast as maximum matching problems on bipartite graphs. Our focus is on resource allocation problems where agents may have restrictions that make them incompatible with some resources. We assume that a Principle chooses a maximum matching randomly so that each agent is matched to a resource with some probability. Agents would like to improve their chances of being matched by modifying their restrictions within certain limits. The Principle's goal is to advise an unsatisfied agent to relax its restrictions so that the total cost of relaxation is within a budget (chosen by the agent) and the increase in the probability of being assigned a resource is maximized. We establish hardness results for some variants of this budget-constrained maximization problem and present algorithmic results for other variants. We experimentally evaluate our methods on synthetic datasets as well as on two novel real-world datasets: a vacation activities dataset and a classrooms dataset.