PAC-Learning for Strategic Classification
Paper and Code
Dec 08, 2020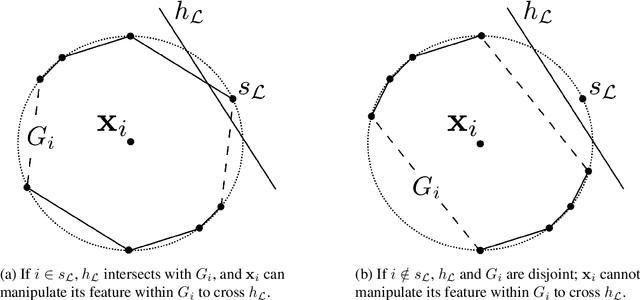
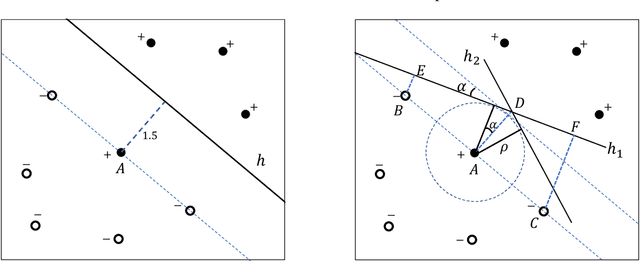
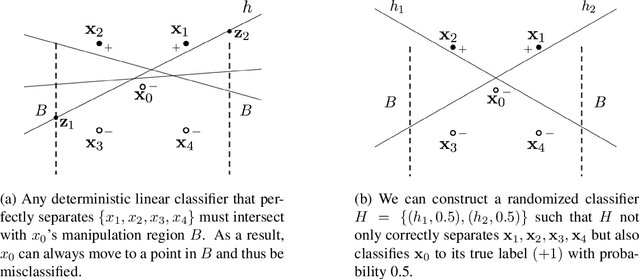
Machine learning (ML) algorithms may be susceptible to being gamed by individuals with knowledge of the algorithm (a.k.a. Goodhart's law). Such concerns have motivated a surge of recent work on strategic classification where each data point is a self-interested agent and may strategically manipulate his features to induce a more desirable classification outcome for himself. Previous works assume agents have homogeneous preferences and all equally prefer the positive label. This paper generalizes strategic classification to settings where different data points may have different preferences over the classification outcomes. Besides a richer model, this generalization allows us to include evasion attacks in adversarial ML also as a special case of our model where positive [resp. negative] data points prefer the negative [resp. positive] label, and thus for the first time allows strategic and adversarial learning to be studied under the same framework. We introduce the strategic VC-dimension (SVC), which captures the PAC-learnability of a hypothesis class in our general strategic setup. SVC generalizes the notion of adversarial VC-dimension (AVC) introduced recently by Cullina et al. arXiv:1806.01471. We then instantiate our framework for arguably the most basic hypothesis class, i.e., linear classifiers. We fully characterize the statistical learnability of linear classifiers by pinning down its SVC and the computational tractability by pinning down the complexity of the empirical risk minimization problem. Our bound of SVC for linear classifiers also strictly generalizes the AVC bound for linear classifiers in arXiv:1806.01471. Finally, we briefly study the power of randomization in our strategic classification setup. We show that randomization may strictly increase the accuracy in general, but will not help in the special case of adversarial classification under evasion attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge