Mika Sarkin Jain
Subsampling Graphs with GNN Performance Guarantees
Feb 23, 2025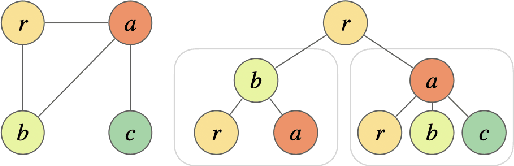
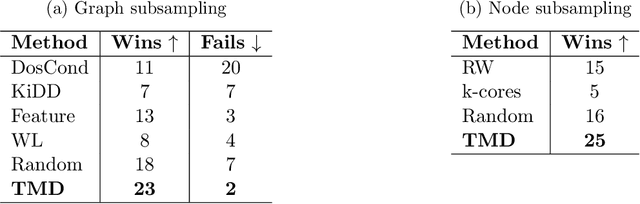
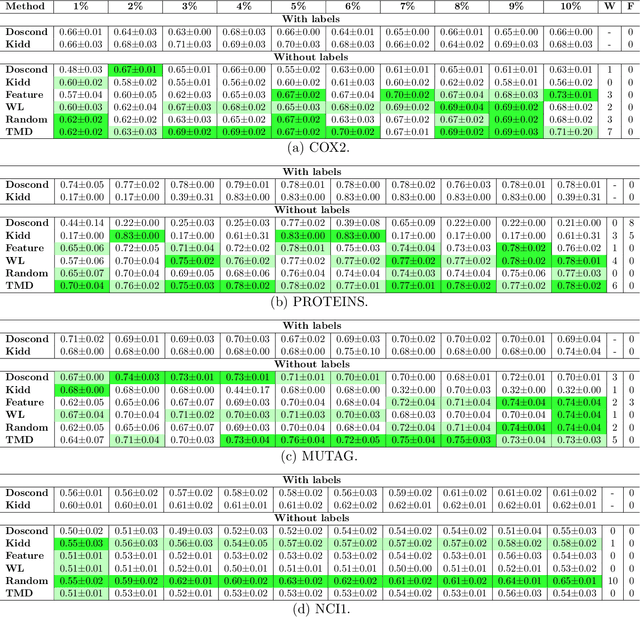
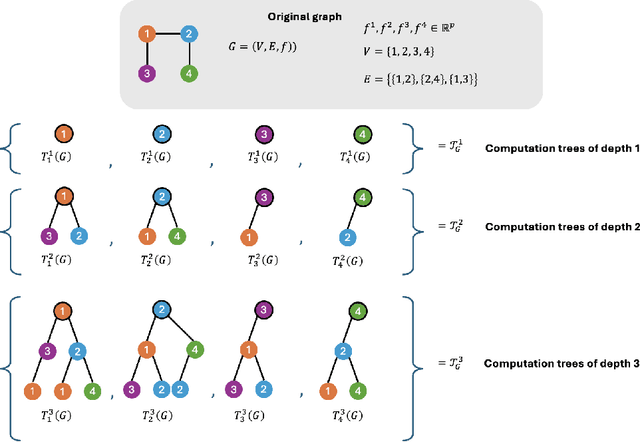
Abstract:How can we subsample graph data so that a graph neural network (GNN) trained on the subsample achieves performance comparable to training on the full dataset? This question is of fundamental interest, as smaller datasets reduce labeling costs, storage requirements, and computational resources needed for training. Selecting an effective subset is challenging: a poorly chosen subsample can severely degrade model performance, and empirically testing multiple subsets for quality obviates the benefits of subsampling. Therefore, it is critical that subsampling comes with guarantees on model performance. In this work, we introduce new subsampling methods for graph datasets that leverage the Tree Mover's Distance to reduce both the number of graphs and the size of individual graphs. To our knowledge, our approach is the first that is supported by rigorous theoretical guarantees: we prove that training a GNN on the subsampled data results in a bounded increase in loss compared to training on the full dataset. Unlike existing methods, our approach is both model-agnostic, requiring minimal assumptions about the GNN architecture, and label-agnostic, eliminating the need to label the full training set. This enables subsampling early in the model development pipeline (before data annotation, model selection, and hyperparameter tuning) reducing costs and resources needed for storage, labeling, and training. We validate our theoretical results with experiments showing that our approach outperforms existing subsampling methods across multiple datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge